
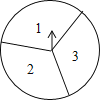
【题目】如图,在一个可以自由转动的转盘中,指针位置固定,三个扇形的面积都相等,且分别标有数字1,2,3.
(1)小明转动转盘一次,当转盘停止转动时,指针所指扇形中的数字是奇数的概率为 .
(2)小明和小颖用转盘做游戏,每人转动转盘一次,若两次指针所指数字之和为奇数,则小明胜,否则小颖胜(指针指在分界线时重转),这个游戏对双方公平吗?请用树状图或者列表法说明理由.
【答案】(1)![]() ;(2)不公平,理由见解析
;(2)不公平,理由见解析
【解析】
(1)由标有数字1、2、3的3个转盘中,奇数的有1、3这2个,利用概率公式计算可得;
(2)根据题意列表得出所有等可能的情况,得出这两个数字之和是奇数与偶数的情况,再根据概率公式即可得出答案.
解:(1)∵在标有数字1、2、3的3个转盘中,奇数的有1、3这2个,
∴指针所指扇形中的数字是奇数的概率为![]() ,
,
故答案为:![]() ;
;
(2)不公平,理由如下:
列表如下:
1 | 2 | 3 | |
1 | 2 | 3 | 4 |
2 | 3 | 4 | 5 |
3 | 4 | 5 | 6 |
由表可知,所有等可能的情况数为9种,其中两次指针所指数字之和为奇数的有4种结果,和为偶数的有5种结果,
所以小明获胜的概率为![]() ,小颖获胜的概率为
,小颖获胜的概率为![]() ,
,
由![]() ≠
≠![]() 知此游戏不公平.
知此游戏不公平.


科目:初中数学 来源: 题型:
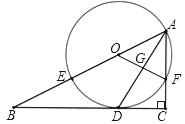
【题目】如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,O为AB上一点,经过点A,D的⊙O分别交AB,AC于点E,F,连接OF交AD于点G.
(1)求证:BC是⊙O的切线;
(2)设AB=x,AF=y,试用含x,y的代数式表示线段AD的长;
(3)若BE=8,sinB=![]() ,求DG的长,
,求DG的长,
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 经过A(﹣1,0),B(3,0)两点,交y轴于点C,点D为抛物线的顶点,连接BD,点H为BD的中点.请解答下列问题:
经过A(﹣1,0),B(3,0)两点,交y轴于点C,点D为抛物线的顶点,连接BD,点H为BD的中点.请解答下列问题:
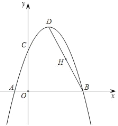
(1)求抛物线的解析式及顶点D的坐标;
(2)在y轴上找一点P,使PD+PH的值最小,则PD+PH的最小值为
查看答案和解析>>
科目:初中数学 来源: 题型:
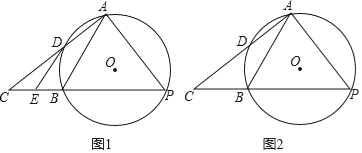
【题目】已知AB是⊙O的弦,点P是优弧AB上的一个动点,连接AP,过点A作AP的垂线,交PB的延长线于点C.
(1)如图1,AC与⊙O相交于点D,过点D作⊙O的切线,交PC于点E,若DE∥AB,求证:PA=PB;
(2)如图2,已知⊙O的半径为2,AB=2![]() .
.
①当点P在优弧AB上运动时,∠C的度数为 °;
②当点P在优弧AB上运动时,△ABP的面积随之变化,求△ABP面积的最大值;
③当点P在优弧AB上运动时,△ABC的面积随之变化,△ABC的面积的最大值为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P从![]() 出发,沿所示方向运动,每当碰到长方形OABC的边时会进行反弹,反弹时反射角等于入射角,当点P第2018次碰到长方形的边时,点P的坐标为______.
出发,沿所示方向运动,每当碰到长方形OABC的边时会进行反弹,反弹时反射角等于入射角,当点P第2018次碰到长方形的边时,点P的坐标为______.

【答案】![]()
【解析】
根据反射角与入射角的定义作出图形;由图可知,每6次反弹为一个循环组依次循环,用2018除以6,根据商和余数的情况确定所对应的点的坐标即可.
解:如图所示:经过6次反弹后动点回到出发点![]() ,
,
![]() ,
,
![]() 当点P第2018次碰到矩形的边时为第337个循环组的第2次反弹,
当点P第2018次碰到矩形的边时为第337个循环组的第2次反弹,
![]() 点P的坐标为
点P的坐标为![]() .
.
故答案为:![]() .
.
【点睛】
此题主要考查了点的坐标的规律,作出图形,观察出每6次反弹为一个循环组依次循环是解题的关键.
【题型】填空题
【结束】
15
【题目】为了保护环境,某公交公司决定购买A、B两种型号的全新混合动力公交车共10辆,其中A种型号每辆价格为a万元,每年节省油量为![]() 万升;B种型号每辆价格为b万元,每年节省油量为
万升;B种型号每辆价格为b万元,每年节省油量为![]() 万升:经调查,购买一辆A型车比购买一辆B型车多20万元,购买2辆A型车比购买3辆B型车少60万元.
万升:经调查,购买一辆A型车比购买一辆B型车多20万元,购买2辆A型车比购买3辆B型车少60万元.
![]() 请求出a和b;
请求出a和b;
![]() 若购买这批混合动力公交车每年能节省
若购买这批混合动力公交车每年能节省![]() 万升汽油,求购买这批混合动力公交车需要多少万元?
万升汽油,求购买这批混合动力公交车需要多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
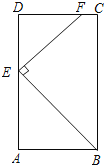
【题目】如图,在矩形ABCD中,AB=6,AD=12,点E在AD边上,且AE=8,EF⊥BE交CD于F.
(1)求证:△ABE∽△DEF;
(2)求EF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:反比例函数![]() 的图象与一次函数
的图象与一次函数![]() 的图象交于
的图象交于![]() 、
、![]() 两点,其中
两点,其中![]() 点坐标为
点坐标为![]() .
.

(1)求反比例函数与一次函数的表达式;
(2)观察图象,直接写出当![]() 时,自变量
时,自变量![]() 的取值范围;
的取值范围;
(3)一次函数的图象与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是反比例函数图象上的一个动点,若
是反比例函数图象上的一个动点,若![]() ,求此时
,求此时![]() 点的坐标.
点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]()
(1)若![]() 求该抛物线与x轴的交点坐标;
求该抛物线与x轴的交点坐标;
(2)若![]() ,是否存在实数
,是否存在实数![]() ,使得相应的y=1,若有,请指明有几个并证明你的结论,若没有,阐述理由。
,使得相应的y=1,若有,请指明有几个并证明你的结论,若没有,阐述理由。
(3)若![]() 且抛物线在
且抛物线在![]() 区间上的最小值是-3,求b的值。
区间上的最小值是-3,求b的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
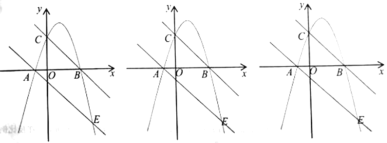
【题目】如图,抛物线![]() 经过
经过![]() ,
,![]() 两点,且与
两点,且与![]() 轴交于点
轴交于点![]() ,抛物线与直线
,抛物线与直线![]() 交于
交于![]() ,
,![]() 两点.
两点.
(1)求抛物线的解析式;
(2)坐标轴上是否存在一点![]() ,使得
,使得![]() 是以
是以![]() 为底边的等腰三角形?若存在,请直接写出点
为底边的等腰三角形?若存在,请直接写出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
(3)![]() 点在
点在![]() 轴上且位于点
轴上且位于点![]() 的左侧,若以
的左侧,若以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似,求点
相似,求点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com