
【题目】已知抛物线![]()
(1)若![]() 求该抛物线与x轴的交点坐标;
求该抛物线与x轴的交点坐标;
(2)若![]() ,是否存在实数
,是否存在实数![]() ,使得相应的y=1,若有,请指明有几个并证明你的结论,若没有,阐述理由。
,使得相应的y=1,若有,请指明有几个并证明你的结论,若没有,阐述理由。
(3)若![]() 且抛物线在
且抛物线在![]() 区间上的最小值是-3,求b的值。
区间上的最小值是-3,求b的值。
【答案】(1)![]() ,
,![]() 和
和![]() ;(2)即存在两个不同实数
;(2)即存在两个不同实数![]() ,使得相应
,使得相应![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)先将a=b=1,c=-1代入y=3ax2+2bx+c,得到抛物线为y=3x2+2x-1,再用因式分解法求出方程3x2+2x-1=0的两个根,即可得到该抛物线与x轴的交点坐标;
(2)将y=1代入y=3ax2+2bx+c,得到3ax2+2bx+c=1,则△=4b2-12a(c-1),再将c-1=-a-b代入△,整理得到△= ,由a≠0,得出△>0,根据一元二次方程根与系数的关系可知方程3ax2+2bx+c=1有两个不相等实数根,即存在两个不同实数x0,使得相应的y=1;
,由a≠0,得出△>0,根据一元二次方程根与系数的关系可知方程3ax2+2bx+c=1有两个不相等实数根,即存在两个不同实数x0,使得相应的y=1;
(3)先将![]() 代入y=3ax2+2bx+c,得到抛物线为y=x2+2bx+b+2,根据二次函数的性质求出其对称轴为x=-b,再分三种情况进行讨论:①x=-b<-2;②x=-b>2;③-2≤-b≤2.
代入y=3ax2+2bx+c,得到抛物线为y=x2+2bx+b+2,根据二次函数的性质求出其对称轴为x=-b,再分三种情况进行讨论:①x=-b<-2;②x=-b>2;③-2≤-b≤2.
解(1)当![]() ,
,![]() 时,抛物线为
时,抛物线为![]() ,
,
∵方程![]() 的两个根为
的两个根为![]() ,
,![]() .
.
∴该抛物线与![]() 轴公共点的坐标是
轴公共点的坐标是![]() 和
和![]() ;
;
(2)存在两个不同实数x0,使得相应的y=1.理由如下:
由![]() 得
得![]() , 即
, 即![]() ,
,
![]()
![]()
![]()
![]()
![]() ,
,
![]() ,
,
∴![]() ,
,
所以方程![]() 有两个不相等实数根,
有两个不相等实数根,
即存在两个不同实数![]() ,使得相应
,使得相应![]() ;
;
(3)![]() ,则抛物线可化为
,则抛物线可化为![]() ,其对称轴为
,其对称轴为![]() ,分三种情况:
,分三种情况:
①当![]() 时,即
时,即![]() ,则有抛物线在
,则有抛物线在![]() 时取最小值为-3,此时
时取最小值为-3,此时![]() ,解得
,解得![]() ,合题意;
,合题意;
②当![]() 时,即
时,即![]() ,则有抛物线在
,则有抛物线在![]() 时取最小值为-3,此时
时取最小值为-3,此时![]() ,解得
,解得![]() ,不合题意,舍去;
,不合题意,舍去;
③当![]() 时,即
时,即![]() ,则有抛物线在
,则有抛物线在![]() 时取最小值为-3,此时
时取最小值为-3,此时![]() ,化简得:
,化简得:![]() ,解得:
,解得:![]() (不合题意,舍去),
(不合题意,舍去),![]() ;
;
综上:![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
【题目】![]() 箱中装有3张相同的卡片,它们分别写有数字1,2,4;
箱中装有3张相同的卡片,它们分别写有数字1,2,4;![]() 箱中也装有3张相同的卡片,它们分别写有数字2,4,5;现从
箱中也装有3张相同的卡片,它们分别写有数字2,4,5;现从![]() 箱、
箱、![]() 箱中各随机地取出1张卡片,请你用画树形(状)图或列表的方法求:
箱中各随机地取出1张卡片,请你用画树形(状)图或列表的方法求:
(1)两张卡片上的数字恰好相同的概率.
(2)如果取出![]() 箱中卡片上的数字作为十位上的数字,取出
箱中卡片上的数字作为十位上的数字,取出![]() 箱中卡片上的数字作为个位上的数字,求两张卡片组成的两位数能被3整除的概率.
箱中卡片上的数字作为个位上的数字,求两张卡片组成的两位数能被3整除的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
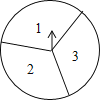
【题目】如图,在一个可以自由转动的转盘中,指针位置固定,三个扇形的面积都相等,且分别标有数字1,2,3.
(1)小明转动转盘一次,当转盘停止转动时,指针所指扇形中的数字是奇数的概率为 .
(2)小明和小颖用转盘做游戏,每人转动转盘一次,若两次指针所指数字之和为奇数,则小明胜,否则小颖胜(指针指在分界线时重转),这个游戏对双方公平吗?请用树状图或者列表法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
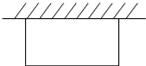
【题目】某农场要建一个长方形的养鸡场,鸡场的一边靠墙,(墙长25m)另外三边用木栏围成,木栏长40m.
(1)若养鸡场面积为200m2,求鸡场靠墙的一边长.
(2)养鸡场面积能达到250m2吗?如果能,请给出设计方案;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学计划购买A型和B型课桌凳共200套,经招标,购买一套A型课桌凳比购买一套B型课桌凳少用40元,,且购买4套A型和6套B型课桌凳共需1820元。
(1)求购买一套A型课桌凳和一套B型课桌凳各需多少元?
(2)学校根据实际情况,要求购买这两种课桌凳总费用不能超过40880元,并且购买A型课桌凳的数量不能超过B型课桌凳的![]() ,求该校本次购买A型和B型课桌凳共有几种方案?哪种方案的总费用最低?
,求该校本次购买A型和B型课桌凳共有几种方案?哪种方案的总费用最低?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,直线
中,直线![]() 与双曲线
与双曲线![]() 相交于点
相交于点![]() .
.
(1)求反比例函数的表达式:
(2)画出直线和双曲线的示意图;
(3)直接写出![]() 的解集______;
的解集______;
(4)若点![]() 是坐标轴负半轴上一点,且满足
是坐标轴负半轴上一点,且满足![]() .直接写出点
.直接写出点![]() 的坐标______.
的坐标______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD沿对角线BD折叠,点C落在点E处,BE交AD于点F,已知∠BDC=62°,则∠DFE的度数为( )
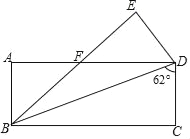
A. 31° B. 28° C. 62° D. 56°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与双曲线
与双曲线![]() 交于
交于![]() 两点,且点
两点,且点![]() 的横坐标为
的横坐标为![]() .
.

(1)求![]() 的值;
的值;
(2)若双曲线![]() 上一点
上一点![]() 的纵坐标为8,求
的纵坐标为8,求![]() 的面积;
的面积;
(3)过原点![]() 的另一条直线
的另一条直线![]() 交双曲线
交双曲线![]() 于
于![]() 两点(
两点(![]() 点在第一象限),若由点
点在第一象限),若由点![]() 为顶点组成的四边形面积为
为顶点组成的四边形面积为![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
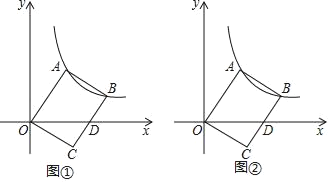
【题目】如图,在平面直角坐标系xOy中,矩形ABCO绕点O旋转,BC边交x轴于点D,反比例函数![]() 经过点A和点B.
经过点A和点B.
(1)如图①,连接AD,若OA=OD=5,且△OAD的面积为10,求反比例函数的解析式;
(2)如图②,连接OB,当∠AOD=60°时,点D恰好是BC的中点,并且△OBD的面积为6![]() ,求OA的长.
,求OA的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com