
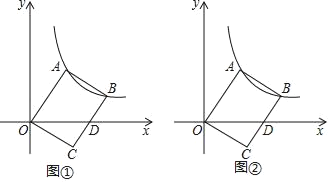
【题目】如图,在平面直角坐标系xOy中,矩形ABCO绕点O旋转,BC边交x轴于点D,反比例函数![]() 经过点A和点B.
经过点A和点B.
(1)如图①,连接AD,若OA=OD=5,且△OAD的面积为10,求反比例函数的解析式;
(2)如图②,连接OB,当∠AOD=60°时,点D恰好是BC的中点,并且△OBD的面积为6![]() ,求OA的长.
,求OA的长.
【答案】(1)![]() ;(2)OA=8.
;(2)OA=8.
【解析】
(1)过点A作AE⊥x轴于点E,利用三角形的面积公式结合△OAD的面积为10,可求出AE的长度,由OA,AE的长利用勾股定理可求出OE的长度,进而可得出点A的坐标,由点A的坐标,再利用待定系数法即可求出反比例函数的解析式;(2)连接AD,过点A作AE⊥x轴于点E,过点B作BF⊥x轴于点F,由平行线的性质可得出∠BDF=∠AOD,结合点D恰好是BC的中点可得出AE=![]() OA,OE=
OA,OE=![]() OA,BF=
OA,BF=![]() OA,DF=
OA,DF=![]() OA,S△OAD=S△OAB=2S△OBD=12
OA,S△OAD=S△OAB=2S△OBD=12![]() .由点A,B在反比例函数图象上结合反比例函数图象上点的坐标特征,可得出OF=OA,进而可得出OD=
.由点A,B在反比例函数图象上结合反比例函数图象上点的坐标特征,可得出OF=OA,进而可得出OD=![]() OA,再利用三角形的面积公式结合S△OAD=12
OA,再利用三角形的面积公式结合S△OAD=12![]() ,可求出OA的长度.
,可求出OA的长度.
(1)在图①中,过点A作AE⊥x轴于点E.
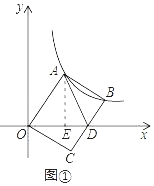
∵S△OAD=![]() ODAE=10,OD=5,
ODAE=10,OD=5,
∴![]() ×5AE=10,
×5AE=10,
∴AE=4,
∴OE=![]() =3,
=3,
∴点A的坐标为(3,4).
将A(3,4)代入y=![]() ,得:4=
,得:4=![]() ,
,
解得:k=12,
∴反比例函数的解析式为y=![]() .
.
(2)在图②中,连接AD,过点A作AE⊥x轴于点E,过点B作BF⊥x轴于点F.
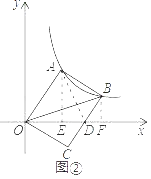
∵OA∥BC,
∴∠BDF=∠AOD=60°.
∵点D恰好是BC的中点,
∴AE=![]() OA,OE=
OA,OE=![]() OA,BF=
OA,BF=![]() OA,DF=
OA,DF=![]() OA,S△OAD=S△OAB=2S△OBD=12
OA,S△OAD=S△OAB=2S△OBD=12![]() .
.
∵反比例函数![]() 经过点A和点B,
经过点A和点B,
∴OEAE=OFBF,
∴OF=2OE=OA,
∴OD=OF﹣DF=![]() OA.
OA.
∴S△OAD=![]() ODAE=
ODAE=![]() OA2=12
OA2=12![]() ,
,
∴OA=8.


科目:初中数学 来源: 题型:
【题目】已知抛物线![]()
(1)若![]() 求该抛物线与x轴的交点坐标;
求该抛物线与x轴的交点坐标;
(2)若![]() ,是否存在实数
,是否存在实数![]() ,使得相应的y=1,若有,请指明有几个并证明你的结论,若没有,阐述理由。
,使得相应的y=1,若有,请指明有几个并证明你的结论,若没有,阐述理由。
(3)若![]() 且抛物线在
且抛物线在![]() 区间上的最小值是-3,求b的值。
区间上的最小值是-3,求b的值。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 经过
经过![]() ,
,![]() 两点,且与
两点,且与![]() 轴交于点
轴交于点![]() ,抛物线与直线
,抛物线与直线![]() 交于
交于![]() ,
,![]() 两点.
两点.
(1)求抛物线的解析式;
(2)坐标轴上是否存在一点![]() ,使得
,使得![]() 是以
是以![]() 为底边的等腰三角形?若存在,请直接写出点
为底边的等腰三角形?若存在,请直接写出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
(3)![]() 点在
点在![]() 轴上且位于点
轴上且位于点![]() 的左侧,若以
的左侧,若以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似,求点
相似,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,小华和小亮想用所学的数学知识测量家门前小河的宽.测量时,他们选择了河对岸边的一棵大树,将其底部作为点A,在他们所在的岸边选择了点B,使得AB与河岸垂直,并在B点竖起标杆BC,再在AB的延长线上选择点D竖起标杆DE,使得点E与点C、A共线.
已知:CB⊥AD,ED⊥AD,测得BC=1m,DE=1.5m,BD=8.5m.测量示意图如图所示.请根据相关测量信息,求河宽AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
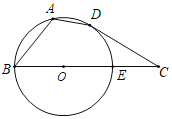
【题目】如图,四边形ABCD的三个顶点A、B、D在⊙O上,BC经过圆心O,且交⊙O于点E,∠A=120°,∠C=30°.
(1)求证:CD是⊙O的切线.
(2)若CD=6,求BC的长.
(3)若⊙O的半径为4,则四边形ABCD的最大面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O过ABCD的三顶点A、D、C,边AB与⊙O相切于点A,边BC与⊙O相交于点H,射线AD交边CD于点E,交⊙O于点F,点P在射线AO上,且∠PCD=2∠DAF.
(1)求证:△ABH是等腰三角形;
(2)求证:直线PC是⊙O的切线;
(3)若AB=2,AD=![]() ,求⊙O的半径.
,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某村耕地总面积为50公顷,且该村人均耕地面积y(单位:公顷/人)与总人口x(单位:人)的函数图象如图所示,则下列说法正确的是( )
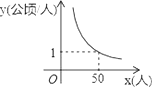
A. 该村人均耕地面积随总人口的增多而增多
B. 该村人均耕地面积y与总人口x成正比例
C. 若该村人均耕地面积为2公顷,则总人口有100人
D. 当该村总人口为50人时,人均耕地面积为1公顷
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 为
为![]() 的直径,
的直径,![]() 为
为![]() 上一点,连接
上一点,连接![]() ,过
,过![]() 作
作![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,其中
,其中![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
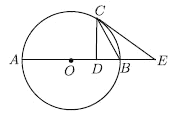
(1)求证:![]() 是
是![]() 的切线.
的切线.
(2)如图,点![]() 在
在![]() 上,且满足
上,且满足![]() ,连接
,连接![]() 并延长交
并延长交![]() 的延长线于点
的延长线于点![]() .
.
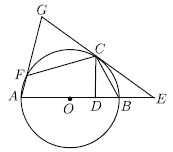
①试探究线段![]() 与
与![]() 之间满足的数量关系.
之间满足的数量关系.
②若![]() ,
,![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | … |
y | … | ﹣6 | 0 | 4 | 6 | 6 | … |
给出下列说法:
①抛物线与y轴的交点为(0,6);
②抛物线的对称轴在y轴的左侧;
③抛物线一定经过(3,0)点;
④在对称轴左侧y随x的增大而减增大.
从表中可知,其中正确的个数为( )
A.4 B.3 C.2 D.1
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com