
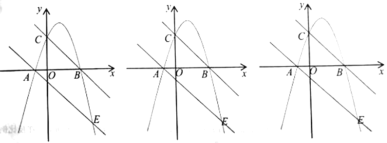
【题目】如图,抛物线![]() 经过
经过![]() ,
,![]() 两点,且与
两点,且与![]() 轴交于点
轴交于点![]() ,抛物线与直线
,抛物线与直线![]() 交于
交于![]() ,
,![]() 两点.
两点.
(1)求抛物线的解析式;
(2)坐标轴上是否存在一点![]() ,使得
,使得![]() 是以
是以![]() 为底边的等腰三角形?若存在,请直接写出点
为底边的等腰三角形?若存在,请直接写出点![]() 的坐标;若不存在,说明理由.
的坐标;若不存在,说明理由.
(3)![]() 点在
点在![]() 轴上且位于点
轴上且位于点![]() 的左侧,若以
的左侧,若以![]() ,
,![]() ,
,![]() 为顶点的三角形与
为顶点的三角形与![]() 相似,求点
相似,求点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)存在,
;(2)存在,![]() 或
或![]() ,理由见解析;(3)
,理由见解析;(3)![]() 或
或![]() .
.
【解析】
(1)将A、C的坐标代入![]() 求出a、c即可得到解析式;
求出a、c即可得到解析式;
(2)先求出E点坐标,然后作AE的垂直平分线,与x轴交于Q,与y轴交于Q',根据垂直平分线的性质可知Q、与A、E,Q'与A、E组成的三角形是以AE为底边的等腰三角形,设Q点坐标(0,x),Q'坐标(0,y),根据距离公式建立方程求解即可;
(3)根据A、E坐标,求出AE长度,然后推出∠BAE=∠ABC=45°,设![]() ,由相似得到
,由相似得到![]() 或
或![]() ,建立方程求解即可.
,建立方程求解即可.
(1)将![]() ,
,![]() 代入
代入![]() 得:
得:
![]() ,解得
,解得![]()
∴抛物线解析式为![]()
(2)存在,理由如下:
联立![]() 和
和![]() ,
,
![]() ,解得
,解得![]() 或
或![]()
∴E点坐标为(4,-5),
如图,作AE的垂直平分线,与x轴交于Q,与y轴交于Q',
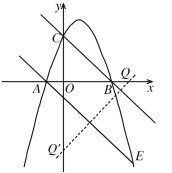
此时Q点与Q'点的坐标即为所求,
设Q点坐标(0,x),Q'坐标(0,y),
由QA=QE,Q'A= Q'E得:
![]() ,
,![]()
解得![]() ,
,![]()
故Q点坐标为![]() 或
或![]()
(3)∵![]() ,
,![]()
∴![]() ,
,
当![]() 时,解得
时,解得![]() 或3
或3
∴B点坐标为(3,0),
∴![]()
∴![]() ,
,![]() ,
,![]() ,
,
由直线![]() 可得AE与y轴的交点为(0,-1),而A点坐标为(-1,0)
可得AE与y轴的交点为(0,-1),而A点坐标为(-1,0)
∴∠BAE=45°
设![]() 则
则![]() ,
,
∵![]() 和
和![]() 相似
相似
∴![]() 或
或![]() ,即
,即![]() 或
或![]()
解得![]() 或
或![]() ,
,
∴![]() 或
或![]() .
.


科目:初中数学 来源: 题型:
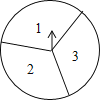
【题目】如图,在一个可以自由转动的转盘中,指针位置固定,三个扇形的面积都相等,且分别标有数字1,2,3.
(1)小明转动转盘一次,当转盘停止转动时,指针所指扇形中的数字是奇数的概率为 .
(2)小明和小颖用转盘做游戏,每人转动转盘一次,若两次指针所指数字之和为奇数,则小明胜,否则小颖胜(指针指在分界线时重转),这个游戏对双方公平吗?请用树状图或者列表法说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD沿对角线BD折叠,点C落在点E处,BE交AD于点F,已知∠BDC=62°,则∠DFE的度数为( )
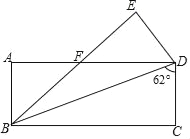
A. 31° B. 28° C. 62° D. 56°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与双曲线
与双曲线![]() 交于
交于![]() 两点,且点
两点,且点![]() 的横坐标为
的横坐标为![]() .
.

(1)求![]() 的值;
的值;
(2)若双曲线![]() 上一点
上一点![]() 的纵坐标为8,求
的纵坐标为8,求![]() 的面积;
的面积;
(3)过原点![]() 的另一条直线
的另一条直线![]() 交双曲线
交双曲线![]() 于
于![]() 两点(
两点(![]() 点在第一象限),若由点
点在第一象限),若由点![]() 为顶点组成的四边形面积为
为顶点组成的四边形面积为![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
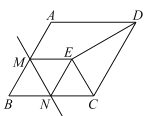
【题目】如图,在菱形![]() 中,
中,![]() 为边
为边![]() 的中点,
的中点,![]() 为边
为边![]() 上一动点(不与
上一动点(不与![]() 重合),将
重合),将![]() 沿直线
沿直线![]() 折叠,使点
折叠,使点![]() 落在点
落在点![]() 处,连接
处,连接![]() ,
,![]() ,当
,当![]() 为等腰三角形时,
为等腰三角形时,![]() 的长为____________.
的长为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
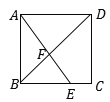
【题目】如图所示,在正方形ABCD中,点E是BC边上一点,且BE:EC=2:1,AE与BD交于点F,则△AFD与四边形DFEC的面积之比是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
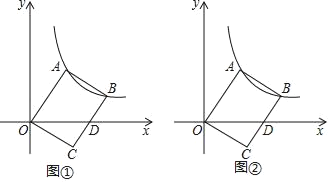
【题目】如图,在平面直角坐标系xOy中,矩形ABCO绕点O旋转,BC边交x轴于点D,反比例函数![]() 经过点A和点B.
经过点A和点B.
(1)如图①,连接AD,若OA=OD=5,且△OAD的面积为10,求反比例函数的解析式;
(2)如图②,连接OB,当∠AOD=60°时,点D恰好是BC的中点,并且△OBD的面积为6![]() ,求OA的长.
,求OA的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
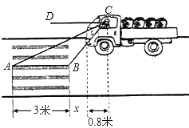
【题目】如图:一辆汽车在一个十字路口遇到红灯刹车停下,汽车里的驾驶员看地面的斑马线前后两端的视角分别是∠DCA=30°和∠DCB=60°,如果斑马线的宽度是AB=3米,驾驶员与车头的距离是0.8米,这时汽车车头与斑马线的距离x是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com