
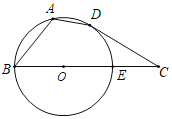
【题目】如图,四边形ABCD的三个顶点A、B、D在⊙O上,BC经过圆心O,且交⊙O于点E,∠A=120°,∠C=30°.
(1)求证:CD是⊙O的切线.
(2)若CD=6,求BC的长.
(3)若⊙O的半径为4,则四边形ABCD的最大面积为 .
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)连接![]() 、
、![]() ,根据圆内接四边形的性质得到
,根据圆内接四边形的性质得到![]() ,求得
,求得![]() ,又点
,又点![]() 在
在![]() 上,于是得到结论;
上,于是得到结论;
(2)由(1)知:![]() 又
又![]() ,设
,设![]() 为
为![]() ,则
,则![]() 为
为![]() ,根据勾股定理即可得到结论;
,根据勾股定理即可得到结论;
(3)连接BD,OA,根据已知条件推出当四边形ABOD的面积最大时,四边形ABCD的面积最大,当OA⊥BD时,四边形ABOD的面积最大,根据三角形和菱形的面积公式即可得到结论.
解:(1)证明:连接![]() 、
、![]() ,
,
![]() 四边形
四边形![]() 为圆内接四边形,
为圆内接四边形,
![]() ,
,
![]() ,
,
![]() ,又点
,又点![]() 在
在![]() 上,
上,
![]() 是
是![]() 的切线;
的切线;
(2)由(1)知:![]() 又
又![]() ,
,
![]()
![]() ,
,
设![]() 为
为![]() ,则
,则![]() 为
为![]() ,
,
在![]() 中,
中,![]() ,
,
即![]() ,
,
![]() ,
,
又![]() ,
,
![]() ,
,
![]() ;
;
(3)连接![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() 当四边形
当四边形![]() 的面积最大时,四边形
的面积最大时,四边形![]() 的面积最大,
的面积最大,
![]() 当
当![]() 时,四边形
时,四边形![]() 的面积最大,
的面积最大,
![]() 四边形
四边形![]() 的最大面积
的最大面积![]() ,
,
故答案为:![]() .
.



科目:初中数学 来源: 题型:
【题目】某中学计划购买A型和B型课桌凳共200套,经招标,购买一套A型课桌凳比购买一套B型课桌凳少用40元,,且购买4套A型和6套B型课桌凳共需1820元。
(1)求购买一套A型课桌凳和一套B型课桌凳各需多少元?
(2)学校根据实际情况,要求购买这两种课桌凳总费用不能超过40880元,并且购买A型课桌凳的数量不能超过B型课桌凳的![]() ,求该校本次购买A型和B型课桌凳共有几种方案?哪种方案的总费用最低?
,求该校本次购买A型和B型课桌凳共有几种方案?哪种方案的总费用最低?
查看答案和解析>>
科目:初中数学 来源: 题型:
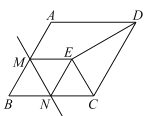
【题目】如图,在菱形![]() 中,
中,![]() 为边
为边![]() 的中点,
的中点,![]() 为边
为边![]() 上一动点(不与
上一动点(不与![]() 重合),将
重合),将![]() 沿直线
沿直线![]() 折叠,使点
折叠,使点![]() 落在点
落在点![]() 处,连接
处,连接![]() ,
,![]() ,当
,当![]() 为等腰三角形时,
为等腰三角形时,![]() 的长为____________.
的长为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
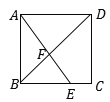
【题目】如图所示,在正方形ABCD中,点E是BC边上一点,且BE:EC=2:1,AE与BD交于点F,则△AFD与四边形DFEC的面积之比是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰![]() 中,
中,![]() .点D,E分别在边AB,BC上,将线段ED绕点E按逆时针方向旋转90得到EF.
.点D,E分别在边AB,BC上,将线段ED绕点E按逆时针方向旋转90得到EF.

(1)如图1,若![]() ,点E与点C重合,AF与DC相交于点O.求证:
,点E与点C重合,AF与DC相交于点O.求证:![]() .
.
(2)已知点G为AF的中点.
①如图2,若![]() ,求DG的长.
,求DG的长.
②若![]() ,是否存在点E,使得
,是否存在点E,使得![]() 是直角三角形?若存在,求CE的长;若不存在,试说明理由.
是直角三角形?若存在,求CE的长;若不存在,试说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
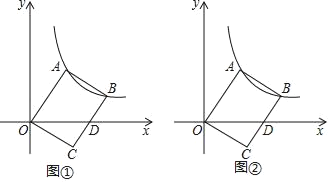
【题目】如图,在平面直角坐标系xOy中,矩形ABCO绕点O旋转,BC边交x轴于点D,反比例函数![]() 经过点A和点B.
经过点A和点B.
(1)如图①,连接AD,若OA=OD=5,且△OAD的面积为10,求反比例函数的解析式;
(2)如图②,连接OB,当∠AOD=60°时,点D恰好是BC的中点,并且△OBD的面积为6![]() ,求OA的长.
,求OA的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小英同时掷甲、乙两枚质地均匀的小立方体(立方体的每个面上分别标有数字1,2,3,4,5,6).记甲立方体朝上一面上的数字为x,乙立方体朝上一面上的数字为y,这样就确定点P的一个坐标(x,y),那么点P落在双曲线y=![]() 上的概率为 .
上的概率为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A,B两地被大山阻隔,若要从A地到B地,只能沿着如图所示的公路先从A地到C地,再由C地到B地.现计划开凿隧道A,B两地直线贯通,经测量得:∠CAB=30°,∠CBA=45°,AC=20km,求隧道开通后与隧道开通前相比,从A地到B地的路程将缩短多少?(结果精确到0.1km,参考数据: ![]() ≈1.414,
≈1.414, ![]() ≈1.732)
≈1.732)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场将进价40元一个的某种商品按50元一个售出时,每月能卖出500个.商场想了两个方案来增加利润:
方案一:提高价格,但这种商品每个售价涨价1元,销售量就减少10个;
方案二:售价不变,但发资料做广告.已知当这种商品每月的广告费用为m(千元)时,每月销售量将是原销售量的p倍,且p =![]() .
.
试通过计算,请你判断商场为赚得更大的利润应选择哪种方案?请说明你判断的理由!
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com