
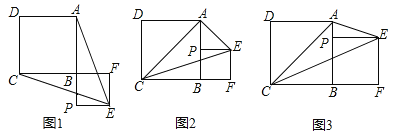
【题目】已知正方形ABCD,P为射线AB上的一点,以BP为边作正方形BPEF,使点F在线段CB的延长线上,连接EA、EC.
(1)如图1,若点P在线段AB的延长线上,求证:EA=EC;
(2)若点P在线段AB上.
①如图2,连接AC,当P为AB的中点时,判断△ACE的形状,并说明理由;
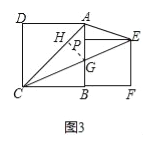
②如图3,设AB=a,BP=b,当EP平分∠AEC时,求a:b及∠AEC的度数.
【答案】(1)详见解析;(2)△ACE为直角三角形,理由见解析;(3)∠AEC=45°.
【解析】试题分析:(1)根据正方形的性质和全等三角形的判定定理易证△APE≌△CFE,由全等三角形的性质即可得结论;(2)①根据正方形的性质、等腰直角三角形的性质即可判定△ACE为直角三角形;②根据PE∥CF,得到![]() ,代入a、b的值计算求出a:b,根据角平分线的判定定理得到∠HCG=∠BCG,证明∠AEC=∠ACB,即可求出∠AEC的度数.
,代入a、b的值计算求出a:b,根据角平分线的判定定理得到∠HCG=∠BCG,证明∠AEC=∠ACB,即可求出∠AEC的度数.
试题解析:(1)证明:∵四边形ABCD为正方形
∴AB=AC
∵四边形BPEF为正方形
∴∠P=∠F=90°,PE=EF=FB=BP
∵AP=AB+BP,CF=BC+BF
∴CF=AP
在△APE和△CFE中:EP="EF," ∠P="∠F=90°," AP= CF
∴△APE≌△CFE
∴EA=EC
(2)①∵P为AB的中点,
∴PA=PB,又PB=PE,
∴PA=PE,
∴∠PAE=45°,又∠DAC=45°,
∴∠CAE=90°,即△ACE是直角三角形;
②∵EP平分∠AEC,EP⊥AG,
∴AP=PG=a﹣b,BG=a﹣(2a﹣2b)=2b﹣a
∵PE∥CF,
∴![]() ,即
,即![]() ,
,
解得,a=![]() b;
b;
作GH⊥AC于H,
∵∠CAB=45°,
∴HG=![]() AG=
AG=![]() ×(2
×(2![]() b﹣2b)=(2﹣
b﹣2b)=(2﹣![]() )b,又BG=2b﹣a=(2﹣
)b,又BG=2b﹣a=(2﹣![]() )b,
)b,
∴GH=GB,GH⊥AC,GB⊥BC,
∴∠HCG=∠BCG,
∵PE∥CF,
∴∠PEG=∠BCG,
∴∠AEC=∠ACB=45°.
∴a:b=![]() :1;∴∠AEC=45°.
:1;∴∠AEC=45°.


科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=acm,AB=bcm(a>b>4),半径为2cm的⊙O在矩形内且与AB、AD均相切,现有动点P从A点出发,在矩形边上沿着A→B→C→D的方向匀速移动,当点P到达D点时停止移动.⊙O在矩形内部沿AD向右匀速平移,移动到与CD相切时立即沿原路按原速返回,当⊙O回到出发时的位置(即再次与AB相切)时停止移动,已知点P与⊙O同时开始移动,同时停止移动(即同时到达各自的终止位置).
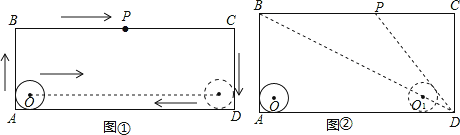
(1)如图①,点P从A→B→C→D,全程共移动了 cm(用含a、b的代数式表示);
(2)如图①,已知点P从A点出发,移动2s到达B点,继续移动3s,到达BC的中点,若点P与⊙O的移动速度相等,求在这5s时间内圆心O移动的距离;
(3)如图②,已知a=20,b=10,是否存在如下情形:当⊙O到达⊙O1的位置时(此时圆心O1在矩形对角线BD上),DP与⊙O1恰好相切?请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于命题“如果∠1+∠2=90°,那么∠1≠∠2”,说明它是假命题的反例可以是( )
A.∠1=50°,∠2=40°
B.∠1=50°,∠2=50°
C.∠1=40°,∠2=40°
D.∠1=∠2=45°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠A=36°,AB=AC,BD平分∠ABC,DE∥BC,则图中等腰三角形的个数( ).
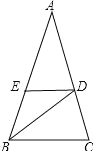
A.1个 B.3个 C.4个 D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某同学把一块三角形的玻璃打碎成了三块,现在要到玻璃店去配一块完全一样的玻璃,那么最省事的办法是( ).
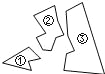
A.带①去 B.带②去 C.带③去 D.带①和②去
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列四组条件中,能判定△ABC≌△DEF的是( )
A. AB=DE,BC= EF,∠A=∠D B. ∠A=∠D,∠C=∠F,AC= DE
C. ∠A=∠E,∠B=∠F,∠C=∠D D. AB=DE,BC= EF,△ABC的周长等于△DEF的周长
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com