
| 类 别 | 电视机 | 洗衣机 |
| 进价(元/台) | 1800 | 1500 |
| 售价(元/台) | 2000 | 1600 |
分析 (1)根据题意列出解析式即可;
(2)关键描述语:电视机进货量不少于洗衣机的进货量的一半,由此可用不等式将电视机和洗衣机的进货量表示出来,再根据商店最多可筹到的资金数可列不等式,求解不等式组即可;
(3)根据利润=售价-进价,列出关系式进行讨论可知哪种方案获利最多
解答 解:(1)y=(2000-1800)x+(1600-1500)(100-x)=100x+10000;
(2)设商店购进电视机x台,则购进洗衣机(100-x)台,
根据题意得$\left\{\begin{array}{l}{x≥\frac{1}{2}(100-x)}\\{1800x+1500(100-x)≤161800}\end{array}\right.$,
解不等式组得$33\frac{1}{3}$≤x≤39$\frac{1}{3}$,
∵x取整数,
∴x可以取34,35,36,37,38,39,
即购进电视机最少34台,最多39台,商店有6种进货方案;
(3)设商店销售完毕后获利为y元,根据题意得
y=(2000-1800)x+(1600-1500)(100-x)=100x+10000.
∵100>0,
∴y随x增大而增大,
∴当x=39时,商店获利最多为13900元.
点评 此题考查一次函数应用,解决问题的关键是读懂题意,找到关键描述语,找到所求的量的等量关系.准确的解不等式是需要掌握的基本计算能力,要熟练掌握利用自变量的取值范围求最值的方法.注意本题的不等关系为:电视机进货量不少于洗衣机的进货量的一半;电视机进货量不少于洗衣机的进货量的一半.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 每小时做的个数 | 所用的时间 | |
| 甲 | x+6 | $\frac{90}{x+6}$ |
| 乙 | x | $\frac{60}{x}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
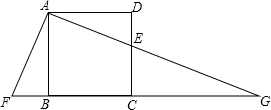 如图,E是正方形ABCD的边DC上的一点,过点A作AF⊥AE,交CB的延长线于点F,AE的延长线交BC的延长线于点G.若AF=13,DE=5,则CG的长是$\frac{84}{5}$.
如图,E是正方形ABCD的边DC上的一点,过点A作AF⊥AE,交CB的延长线于点F,AE的延长线交BC的延长线于点G.若AF=13,DE=5,则CG的长是$\frac{84}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | m>$\frac{9}{8}$ | B. | m≥$\frac{9}{8}$ | C. | m≤$\frac{9}{8}$ | D. | m<$\frac{9}{8}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com