
| 每小时做的个数 | 所用的时间 | |
| 甲 | x+6 | $\frac{90}{x+6}$ |
| 乙 | x | $\frac{60}{x}$ |
分析 (1)设乙每小时做x个,则甲每小时做(x+6)个,甲做90个所用的时间为$\frac{90}{x+6}$,乙做60个所用的时间为$\frac{60}{x}$;
(2)根据甲做90个所用的时间与乙做60个所用的时间相等,列方程求解.
解答 解:(1)设乙每小时做x个,则甲每小时做(x+6)个,
甲做90个所用的时间为$\frac{90}{x+6}$,乙做60个所用的时间为$\frac{60}{x}$;
(2)列方程为:$\frac{90}{x+6}$=$\frac{60}{x}$,
解得:x=12,
经检验:x=12是原分式方程的解,且符合题意,
则x+6=18.
答:甲每小时做18个,乙每小时做12个.
故答案为:x+6,$\frac{90}{x+6}$,$\frac{60}{x}$.
点评 本题考查了分式方程的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程求解,注意检验.


科目:初中数学 来源: 题型:选择题
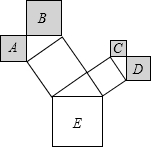 如图是一棵勾股树,它是由正方形和直角三角形拼成的额,若正方形A、B、C、D的边长分别是3、5、2、3,则最大正方形E的面积是( )
如图是一棵勾股树,它是由正方形和直角三角形拼成的额,若正方形A、B、C、D的边长分别是3、5、2、3,则最大正方形E的面积是( )| A. | 47 | B. | 13 | C. | 26 | D. | 94 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 类 别 | 电视机 | 洗衣机 |
| 进价(元/台) | 1800 | 1500 |
| 售价(元/台) | 2000 | 1600 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com