
����Ŀ����ͼ1��ֱ��![]() ��
��![]() ���ڵ�A����
���ڵ�A����![]() ���ڵ�C��0,4��.������
���ڵ�C��0,4��.������![]()
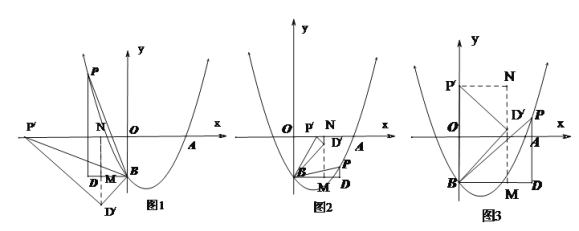
������A����![]() ���ڵ�B��0��-2��.��PΪ��������һ�����㣬������P��
���ڵ�B��0��-2��.��PΪ��������һ�����㣬������P��![]() ��Ĵ���PD������B��BD��PD�ڵ�D������PB�����P�ĺ�����Ϊ
��Ĵ���PD������B��BD��PD�ڵ�D������PB�����P�ĺ�����Ϊ![]() .
.
��1���������ߵĽ���ʽ��
��2������BDPΪ����ֱ��������ʱ�����߶�PD�ij���
��3����ͼ2������BDP�Ƶ�B��ʱ����ת���õ���BD��P��������ת����PBP��=��OAC������P�Ķ�Ӧ��P��������������ʱ����ֱ��д����P������.



���𰸡�(1)![]() ����2������BPDΪ����ֱ��������ʱ��PD�ij�Ϊ
����2������BPDΪ����ֱ��������ʱ��PD�ij�Ϊ![]() .(3)
.(3)![]() ,
,![]() ,
,![]() .
.
��������
���������(1)����õ�A�����꣬�����ô���ϵ�����������ߵĽ���ʽ���ɣ���2�����P�ĺ�����Ϊ![]() ,�ɵ�P(m��
,�ɵ�P(m��![]() )��D(m��-2)������BPDΪ����ֱ�������Σ���PD=BD.�����������������P��ֱ��BD���Ϸ�ʱ��PD=
)��D(m��-2)������BPDΪ����ֱ�������Σ���PD=BD.�����������������P��ֱ��BD���Ϸ�ʱ��PD=![]() ,�ٷֵ�P��y��������Ҳ�����������з�����⼴�ɣ�������P��ֱ��BD���·�ʱ��m��0��BD=m��PD=
,�ٷֵ�P��y��������Ҳ�����������з�����⼴�ɣ�������P��ֱ��BD���·�ʱ��m��0��BD=m��PD=![]() ,�з�����⼴�ɣ���3���ߡ�PBP/=��OAC,OA=3,OC=4����AC=5����sin��PBP/=
,�з�����⼴�ɣ���3���ߡ�PBP/=��OAC,OA=3,OC=4����AC=5����sin��PBP/=![]() ��cos��PBP/=
��cos��PBP/=![]() ��������P/����x����ʱ������D/��D/N��x����N����BD�ڵ�M����DBD/=��ND/P/=��PBP/,��ͼ1��ND/-MD/=2,��
��������P/����x����ʱ������D/��D/N��x����N����BD�ڵ�M����DBD/=��ND/P/=��PBP/,��ͼ1��ND/-MD/=2,��![]() ��(
��(![]() m2-
m2-![]() m)-��-
m)-��-![]() m��=2����ͼ2��ND/-MD/=2����
m��=2����ͼ2��ND/-MD/=2����![]() ��(
��(![]() m2-
m2-![]() m)-��-
m)-��-![]() m��=2��ã�P����
m��=2��ã�P����![]() ��
��![]() ����P��
����P��![]() ��
��![]() ����������P/����y����ʱ��
����������P/����y����ʱ��
��ͼ3������D/��D/M��x�ύBD�ڵ�M������P/��P/N��y�ᣬ��MD/���ӳ����ڵ�N����DBD/=��ND/P/=��PBP/,��PN=BM,�� ![]() ��(
��(![]() m2-
m2-![]() m)=
m)= ![]() m��P��
m��P��![]() ��
��![]() ��
��
���������(1)��ֱ��![]() ����C��0,4������n=4����
����C��0,4������n=4����![]() .
.
��y=0ʱ��![]() �����x=3����A��3,0��.
�����x=3����A��3,0��.
��������![]() ������A��3,0����B��0��-2����
������A��3,0����B��0��-2����
�� �����
�����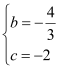
��![]() .
.
(2)���P�ĺ�����Ϊ![]() ,��P(m��
,��P(m��![]() )��D(m��-2).
)��D(m��-2).
����BPDΪ����ֱ�������Σ���PD=BD.
������P��ֱ��BD���Ϸ�ʱ��PD=![]() ,
,
(I)����P��y�����࣬��m��0��BD=-m��
��![]() ��
��
���![]() ����ȥ��.
����ȥ��.
(II)����P��y����Ҳ࣬��m��0��BD=m��
��![]() ��
��
���![]() .
.
������P��ֱ��BD���·�ʱ��m��0��BD=m��PD=![]() ,
,
��![]() ��
��
���![]() .
.
����m=![]() .
.
������BPDΪ����ֱ��������ʱ��PD�ij�Ϊ![]() .
.
(3)![]() ,
,![]() ,
,![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
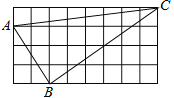
����Ŀ����ͼ�����������еġ�ABC,��С����߳�Ϊ1,���������ѧ��֪ʶ
��1�����ABC�������
��2���жϡ�ABC��ʲô��״? ��˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
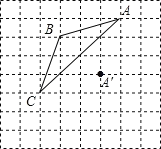
����Ŀ����ͼ��������������ÿ��С�����εı߳�Ϊ1�������ABC�Ķ���A��1��2����B����2��1���� ����ABCƽ�Ƶõ���A��B��C����ʹ�õ�A�Ķ�Ӧ��A�����Խ���������⣺
��1���������⣬�������н���ƽ��ֱ������ϵ��
��2��������A��B��C������д����C��������Ϊ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ô���ʽ��ʾ��a��3����b��ƽ���IJ�������ȷ������ ��
A. ��3a��b��2 B. 3��a��b��2 C. ��a��3b��2 D. 3a��b2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��(2016����ʡ�����е�20��)����ijѧУ��չ��Զ�Ǿ�ɽ��ĥ����־���������࣬��������Ϊ�����Զ������֪ѧУ���ɽ�����24ǧ�ף�Զ�������Ա�����г���ѧ�����У�������Ա�����г���ƽ���ٶ���ѧ������ƽ���ٶȵ�2.5����������Ա��ѧ��ͬʱ��ѧУ�����������ɽ��ʱ��������Ա����ʱ���ѧ��������3.6Сʱ����ѧ�����е�ƽ���ٶ��Ƕ���ǧ��/Сʱ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��x=1�Ƿ���3x��m+1=0�Ľ�����m��ֵ�ǣ��� ��
A. ��4 B. 4 C. 2 D. ��2
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com