

���� ��1�����������õ�E�͵�A������ΪE��-$\frac{b}{2}$��0����A��0��b�������ݡ�AOE�����=$\frac{1}{2}$|OE|•|OA|=$\frac{1}{2}$|-$\frac{b}{2}$|•|b|=4���������b��ֵ��
��2������D��DF��ֱ��x����F������C��CH��ֱ��DF��H�����ݹ��ɶ������AE=2$\sqrt{5}$��֤��AOΪ��DEF����λ�ߣ��õ�OF=OE=2��DF=2OA=2��4=8�����ɵ���Rt��ADC��AD=CD����ADC=90�㣬�õ�CD=2$\sqrt{5}$��ֱ��CD��б��Ϊ-$\frac{1}{2}$����tan��DCH=|-$\frac{1}{2}$|=$\frac{1}{2}$����Rt��CDH�У����DH=CD•sin��DCH=2$\sqrt{5}$•$\frac{1}{\sqrt{5}}$=2��CH=CD•cos��DCH=2$\sqrt{5}$•$\frac{2}{\sqrt{5}}$=4�����Ե�C��x������ΪCH+OF=4+2=6��y������ΪDF-DH=8-2=6�����ɽ��
��3��P��λ�ò������ı䣬���ݵ���Rt��ADC��AD=CD���õ���DAC=45�㣬��ֱ��y=2x+4��֪tan��AEO=2�����ͼ2��ֱ֪��AC��б�� k=tan����AEO-��DAC��=$\frac{tan��AEO-tan��DAC}{1+tan��AEO•tan��DAC}$=$\frac{2-1}{1+2}$=$\frac{1}{3}$���ɣ�1��֪����A��0��4��������ֱ��AC�ķ���Ϊ��y=$\frac{1}{3}$x+4����y=0�����x=-12�����Ե�P��-12��0������ֱ��AC�ķ��̿�֪����P�������D���˶����ı䣮
��� �⣺��1����y=2x+b����x=0ʱ��y=b����y=0ʱ��x=-$\frac{b}{2}$��
���E�͵�A������ΪE��-$\frac{b}{2}$��0����A��0��b����
�ߡ�AOE�����=$\frac{1}{2}$|OE|•|OA|=$\frac{1}{2}$|-$\frac{b}{2}$|•|b|=$\frac{{b}^{2}}{4}$=4
��ã�b=��4��
��ͼ�ж�b=-4�������⣬
��b=4��
��2����ͼ1������D��DF��ֱ��x����F������C��CH��ֱ��DF��H��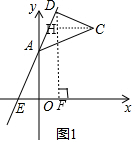
��y=2x+4����y=0ʱ��x=-2��
��OE=2��OA=4��
��AE=$\sqrt{{2}^{2}+{4}^{2}}=2\sqrt{5}$��
��DF��x�ᣬ��AOE=90�㣬
��AO��DF��
����Rt��DEF��AD=AE��
��OF=OE=2��DF=2OA=2��4=8��
�֡ߵ���Rt��ADC��AD=CD����ADC=90�㣬
��CD=2$\sqrt{5}$��ֱ��CD��б��Ϊ-$\frac{1}{2}$����tan��DCH=|-$\frac{1}{2}$|=$\frac{1}{2}$
����Rt��CDH�У�DH=CD•sin��DCH=2$\sqrt{5}$•$\frac{1}{\sqrt{5}}$=2��
CH=CD•cos��DCH=2$\sqrt{5}$•$\frac{2}{\sqrt{5}}$=4��
���C��x������ΪCH+OF=4+2=6��
y������ΪDF-DH=8-2=6��
����C��6��6����
��3��P��λ�ò������ı䣬
�ߵ���Rt��ADC��AD=CD��
���DAC=45��
��ֱ��y=2x+4��֪tan��AEO=2
���ͼ2��ֱ֪��AC��б�ʣ�
k=tan����AEO-��DAC��=$\frac{tan��AEO-tan��DAC}{1+tan��AEO•tan��DAC}$=$\frac{2-1}{1+2}$=$\frac{1}{3}$��
�ɣ�1��֪����A��0��4��
����ֱ��AC�ķ���Ϊ��y=$\frac{1}{3}$x+4
��y=0�����x=-12
���Ե�P��-12��0��
��ֱ��AC�ķ��̿�֪����P�������D���˶����ı䣮
���� ���⿼����һ�κ��������ʡ����������ε����ʡ����ɶ��������Ǻ����������2���Ĺؼ������������ߣ����������Ǻ������CH��DH�ij��ȣ�����ȷ����C�����꣮


 ������������ϵ�д�
������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
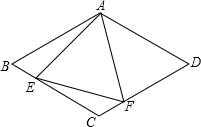 ��ͼ��������ABCD�У�AB=4����BAD=120�㣬��AEFΪ�������Σ���E��F�ֱ������εı�BC��CD�ϻ�������E��F����B��C��D�غϣ�
��ͼ��������ABCD�У�AB=4����BAD=120�㣬��AEFΪ�������Σ���E��F�ֱ������εı�BC��CD�ϻ�������E��F����B��C��D�غϣ��鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
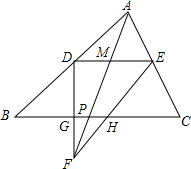 ��ͼ���ڡ�ABC�У�DE��BC��PΪBC��һ�㣬F��AP�ӳ�����һ�㣬FD��FE�ֱ�BC�ڵ�G��H����֤��$\frac{PG}{PB}=\frac{PH}{PC}$��
��ͼ���ڡ�ABC�У�DE��BC��PΪBC��һ�㣬F��AP�ӳ�����һ�㣬FD��FE�ֱ�BC�ڵ�G��H����֤��$\frac{PG}{PB}=\frac{PH}{PC}$���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a2=b2+c2+2bccosA | B�� | a2=b2+c2+bccosA | ||
| C�� | a2=b2+c2-2bccosA | D�� | a2=b2+c2-2bcsinA |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬B�����꣨5��0����MΪ��������OBCD�ױ�OB��һ�㣬OD=BC=2����DMC=��DOB=60��
��ͼ����ƽ��ֱ������ϵ�У�OΪ����ԭ�㣬B�����꣨5��0����MΪ��������OBCD�ױ�OB��һ�㣬OD=BC=2����DMC=��DOB=60���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
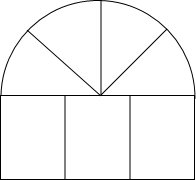 �ӷ��ݵĴ�������״��ͼ��ʾ�������ϲ����ĸ�С������ɵİ�Բ���²�����������ͬ��С������ɣ���������IJ����ܳ�Ϊ15m�����Բ�İ뾶Ϊxm�������Ľ������ΪSm2��
�ӷ��ݵĴ�������״��ͼ��ʾ�������ϲ����ĸ�С������ɵİ�Բ���²�����������ͬ��С������ɣ���������IJ����ܳ�Ϊ15m�����Բ�İ뾶Ϊxm�������Ľ������ΪSm2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
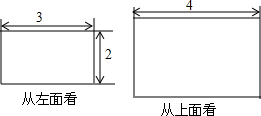 һ������������濴�����濴�������������ͼ��ʾ����������濴����ͼ������ǣ�������
һ������������濴�����濴�������������ͼ��ʾ����������濴����ͼ������ǣ�������| A�� | 6 | B�� | 8 | C�� | 12 | D�� | 24 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com