Question

11．如图，在平面直角坐标系中，O为坐标原点，B的坐标（5，0），M为等腰梯形OBCD底边OB上一点，OD=BC=2，∠DMC=∠DOB=60°
（1）求直线CB的解析式；
（2）求点M的坐标；
（3）∠DMC绕点M顺时针旋转a（30°＜a＜60°）后，得到∠D₁MC₁（点D₁、C₁依次与点D、C对应），射线MC₁交直线CB于点F．设DE=m，BF=n，求m与n的函数关系式．

Answer 1

分析 （1）如图1所示；过点C作CE⊥OB，垂足为E．由等腰梯形的性质可知∠CBO=∠DOB=60°，由特殊锐角三角函数可求得EC=$\sqrt{3}$，BE=1，最后点B和点C的坐标可求得CB的解析式；
（2）如图2所示；过点C作CE⊥OB，垂足为E，过点D作DF⊥OB，垂足为F，连接ED、CF．证明∠DEC=60°，∠DFC=60°，从而可知点M与点E或点F重合；
（3）如图3和图4，先证明△DEM∽△CFM，然后利用相似三角形的性质列出关于m、n的比例式，从而可得出m与n的函数关系式．

解答 解：（1）如图1所示；过点C作CE⊥OB，垂足为E．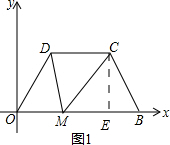

∵梯形OBCD为等腰梯形，
∴∠CBO=∠DOB=60°．
∴EC=sin60°•BC=$\frac{\sqrt{3}}{2}×2$=$\sqrt{3}$，BE=cos60°•BC=$\frac{1}{2}×2$=1．
∴点C的坐标为（4，$\sqrt{3}$）．
设直线BC的解析式为y=kx+b，将点B和点C的坐标代入得：$\left\{\begin{array}{l}{4k+b=\sqrt{3}}\\{5k+b=0}\end{array}\right.$，
解得：k=$-\sqrt{3}$，b=5$\sqrt{3}$．
∴直线BC的解析式为y=-$\sqrt{3}x$+5$\sqrt{3}$．
（2）如图2所示；过点C作CE⊥OB，垂足为E，过点D作DF⊥OB，垂足为F，连接ED、CF．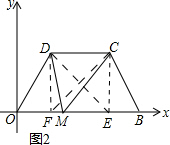

由（1）可知点C的坐标为（4，$\sqrt{3}$）．
同理可知点F的坐标为（1，$\sqrt{3}$）．
∴DC=3，CE=DF=$\sqrt{3}$．
∵在Rt△DCE中，tan∠DEC=$\frac{DC}{CE}=\frac{3}{\sqrt{3}}=\sqrt{3}$，
∴∠DEC=60°．
同理∠DFC=60°．
∵∠DMC=60°，
∴点M与点E或点F重合．
∴点M的坐标为（1，0）或（4，0）．
（3）①当M的为坐标为（1，0）时，如图3所示：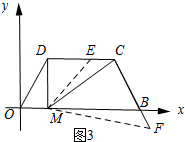

∵在Rt△DCM中，∠DMC=60°，DM=$\sqrt{3}$，
∴MC=2$\sqrt{3}$．
∵由（2）可知∠OMD=90°，∠DMC=60°，
∴∠CMB=30°．
∵由（1）可知∠OBC=60°，
∴∠MCB=90°．
∴∠MDE=∠MCF．
又∵∠DME=∠CMF，
∴△DEM∽△CFM．
∴$\frac{DE}{CF}=\frac{DM}{MC}$，即$\frac{m}{n+2}=\frac{\sqrt{3}}{2\sqrt{3}}$．
∴m与n的函数关系式为m=$\frac{1}{2}n+1$．
②当M的为坐标为（4，0）时，如图4所示：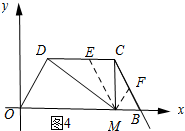

∵在Rt△DCM中，∠DMC=60°，CM=$\sqrt{3}$，
∴DM=2$\sqrt{3}$．
∵∠MCD=90°，∠DMC=60°，
∴∠CDM=30°．
∵由（1）可知∠OBC=60°，
∴∠MCB=30°．
∴∠MDE=∠MCF．
又∵∠DME=∠CMF，
∴△DEM∽△CFM．
∴$\frac{DE}{CF}=\frac{DM}{MC}$，即$\frac{m}{2-n}=\frac{2\sqrt{3}}{\sqrt{3}}$．
∴m与n的函数关系式为m=-2n+4．
综上所述，当M的为坐标为（4，0）时，m与n的函数关系式为m=$\frac{1}{2}n+1$；当M的为坐标为（4，0）时，m与n的函数关系式为m=-2n+4．

点评 本题主要考查的是一次函数的综合应用、特殊锐角三角函数值、等腰梯形的性质、相似三角形的性质和判定、旋转的性质，掌握梯形中辅助线的做法以及证得△DEM∽△CFM是解题的关键．