

分析 (1)延长EB交DG于点H,先证出Rt△ADG≌Rt△ABE,得出∠AGD=∠AEB,再根据∠HBG=∠EBA,得出∠HGB+∠HBG=90°即可;
(2)过点A作AP⊥BD交BD于点P,根据△DAG≌△BAE得出DG=BE,∠APD=90°,求出AP、DP,利用勾股定理求出PG,再根据DG=DP+PG求出DG,最后根据DG=BE即可得出答案.
解答 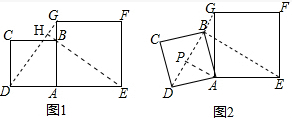 解:(1)如图1,延长EB交DG于点H,
解:(1)如图1,延长EB交DG于点H,
∵ABCD和AEFG为正方形,
∴在Rt△ADG和Rt△ABE中,
$\left\{\begin{array}{l}{AB=AD}\\{∠GAD=∠GAE}\\{AE=AG}\end{array}\right.$,
∴Rt△ADG≌Rt△ABE,
∴∠AGD=∠AEB,
∵∠HBG=∠EBA,
∴∠HGB+∠HBG=90°,
∴DG⊥BE;
(2)如图2,过点A作AP⊥BD交BD于点P,
∵ABCD和AEFG为正方形,
∴在△DAG和△BAE中,
$\left\{\begin{array}{l}{AD=AB}\\{∠DAG=∠BAE}\\{AE=AG}\end{array}\right.$,
∴△DAG≌△BAE(SAS),
∴DG=BE,
∵∠APD=90°,
∴AP=DP=$\sqrt{2}$,
∵AG=2$\sqrt{2}$,
∴PG=$\sqrt{A{G}^{2}-P{A}^{2}}$=$\sqrt{6}$,
∴DG=DP+PG=$\sqrt{2}$+$\sqrt{6}$,
∵DG=BE,
∴BE=$\sqrt{2}$+$\sqrt{6}$.
点评 此题考查了旋转的性质和正方形的性质,用到的知识点是旋转的性质、全等三角形的判定,勾股定理和正方形的性质,关键是根据题意画出辅助线,构造直角三角形.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:初中数学 来源: 题型:填空题
 如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE.延长EF交边BC于点G,连接AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③AG∥CF;④△GCF是等边三角形,其中正确结论有①②③.
如图,正方形ABCD中,AB=6,点E在边CD上,且CD=3DE,将△ADE沿AE对折至△AFE.延长EF交边BC于点G,连接AG、CF.下列结论:①△ABG≌△AFG;②BG=GC;③AG∥CF;④△GCF是等边三角形,其中正确结论有①②③.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在平面直角坐标系中,点C、D在反比例函数y=$\frac{k}{x}$(x>0)的图象上,过点D作BA∥x轴交y轴于点A,BC∥y轴且交曲线于点C,已知BD=3AD,若四边形ODBC的面积为6,则k=2.
如图,在平面直角坐标系中,点C、D在反比例函数y=$\frac{k}{x}$(x>0)的图象上,过点D作BA∥x轴交y轴于点A,BC∥y轴且交曲线于点C,已知BD=3AD,若四边形ODBC的面积为6,则k=2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
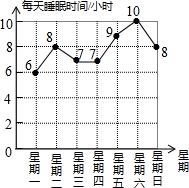 如今中学生睡眠不足的问题正愈演愈烈,“缺觉”已是全国中学生们的老大难问题,教育部规定,初中生每天的睡眠时间应为9个小时,鹏鹏记录了他一周的睡眠时间,并将统计结果绘制成如图所示的折线统计图,则鹏鹏这一周的睡眠够9个小时的有( )
如今中学生睡眠不足的问题正愈演愈烈,“缺觉”已是全国中学生们的老大难问题,教育部规定,初中生每天的睡眠时间应为9个小时,鹏鹏记录了他一周的睡眠时间,并将统计结果绘制成如图所示的折线统计图,则鹏鹏这一周的睡眠够9个小时的有( )| A. | 1天 | B. | 2天 | C. | 3天 | D. | 4天 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,直线y1=mx与双曲线y2=$\frac{k}{x}$相交于点A、B,四边形AODC为菱形,点C在x轴正半轴上,点D的坐标为(2,-3).
如图,在平面直角坐标系中,直线y1=mx与双曲线y2=$\frac{k}{x}$相交于点A、B,四边形AODC为菱形,点C在x轴正半轴上,点D的坐标为(2,-3).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
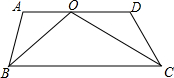 如图所示,AD∥BC,BO,CO分别平分∠ABC,∠DCB,若∠A+∠D=220°,则∠BOC的大小为( )
如图所示,AD∥BC,BO,CO分别平分∠ABC,∠DCB,若∠A+∠D=220°,则∠BOC的大小为( )| A. | 110° | B. | 120° | C. | 130° | D. | 140° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com