
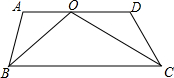
 如图所示,AD∥BC,BO,CO分别平分∠ABC,∠DCB,若∠A+∠D=220°,则∠BOC的大小为( )
如图所示,AD∥BC,BO,CO分别平分∠ABC,∠DCB,若∠A+∠D=220°,则∠BOC的大小为( )| A. | 110° | B. | 120° | C. | 130° | D. | 140° |
分析 根据平行线的性质得出∠A+∠ABC=180°,∠D+∠DCB=180°,求出∠ABC+∠DCB=140°,根据角平分线定义得出∠OBC=$\frac{1}{2}$∠ABC,∠OCB=$\frac{1}{2}$∠DCB,求出∠OBC+∠OCB=70°,根据三角形内角和定理求出即可.
解答 解:∵AD∥BC,
∴∠A+∠ABC=180°,∠D+∠DCB=180°,
∵∠A+∠D=220°,
∴∠ABC+∠DCB=140°,
∵BO,CO分别平分∠ABC,∠DCB,
∴∠OBC=$\frac{1}{2}$∠ABC,∠OCB=$\frac{1}{2}$∠DCB,
∴∠OBC+∠OCB=$\frac{1}{2}$×140°=70°,
∴∠BOC=180°-(∠OBC+∠OCB)=110°,
故选A.
点评 本题考查了平行线的性质,角平分线定义的应用,能灵活运用性质进行推理是解此题的关键,注意:平行线的性质有:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补.


 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
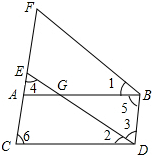 如图,∠1=∠2,∠3=∠4,∠5=∠6.求证:ED∥FB.在下面的括号中填上推理依据.
如图,∠1=∠2,∠3=∠4,∠5=∠6.求证:ED∥FB.在下面的括号中填上推理依据.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
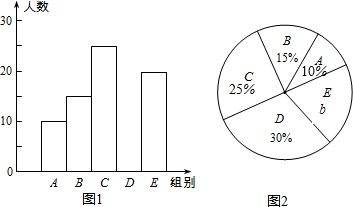 某中学举行“汉字听写”比赛,每位学生听写汉字39个,比赛结束后,随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图的一部分,根据信息解决下列问题:
某中学举行“汉字听写”比赛,每位学生听写汉字39个,比赛结束后,随机抽查部分学生的听写结果,以下是根据抽查结果绘制的统计图的一部分,根据信息解决下列问题:| 组别 | 正确字数x | 人数 |
| A | 0≤x<8 | 10 |
| B | 8≤x<16 | 15 |
| C | 16≤x<24 | 25 |
| D | 24≤x<32 | a |
| E | 32≤x<40 | 20 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com