
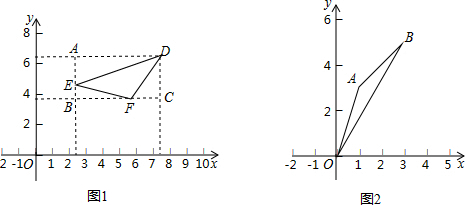
分析 (1)在图2中作出△OAB的投影矩形ACBD,根据投影比的定义即可得出结论;
(2)设出D点的坐标,分0≤x≤2和x<0两种情况考虑,找出两种情况下△OCD的投影矩形,根据投影比的定义列出关于x的方程,解方程即可得出结论;
(3)根据题意画出图形,根据投影矩形的不同分四种情况考虑(m≤1,1<m<3,3≤m≤5和m>5),找出每种情况下的投影矩形投影比,根据m的取值范围确定k的取值范围,由此即可得出结论.
解答 解:(1)在图2中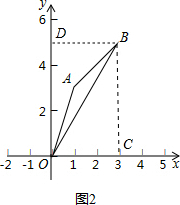
过点B作BC⊥x轴于点C,作BD⊥y轴于点D,则矩形ACBD为△OAB的投影矩形,
∵点B(3,5),
∴OC=3,BC=5,
∴△OAB投影比k的值为$\frac{BC}{OC}$=$\frac{5}{3}$.
(2)∵点D为函数y=2x-4(其中x<2)的图象上的点,
设点D坐标为(x,2x-4)(x<2).
分以下两种情况:
①当0≤x≤2时,如图3所示,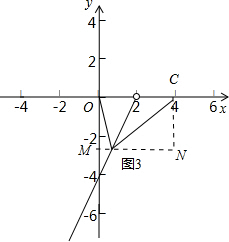
作投影矩形OMNC.
∵OC≥OM,
∴$k=\frac{OC}{OM}=\frac{4}{OM}=\frac{4}{-(2x-4)}=2$,
解得x=1,
∴D(1,-2);
②当x<0时,如图4所示,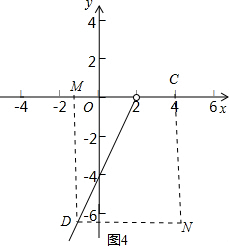
作投影矩形MDNC.
∵点D坐标为(x,2x-4),点M点坐标为(x,0),
∴DM=|2x-4|=4-2x,MC=4-x,
∵x<0,
∴DM>CM,
∴$k=\frac{DM}{MC}=\frac{4-2x}{4-x}=2$,但此方程无解.
∴当x<0时,满足条件的点D不存在.
综上所述,点D的坐标为D(1,-2).
(3)令y=x+1中y=2,则x+1=2,解得:x=1.
①当m≤1时,作投影矩形A′FB′P,如图5所示.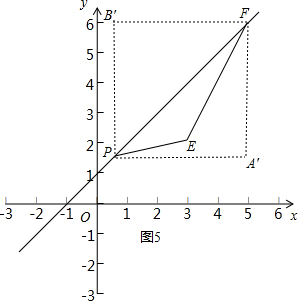
此时点P(m,m+1),PA′=5-m,FA′=6-(m+1)=5-m,△PEF的投影比k=$\frac{FA′}{PA′}$=1,
∴m≤1不符合题意;
②当1<m<3时,作投影矩形A′FB′Q,如图6所示.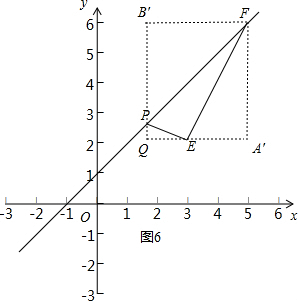
此时点P(m,m+1),FB′=5-m,FA′=6-2=4,△PEF的投影比k=$′\frac{FA′}{FB′}$=$\frac{4}{5-m}$,
∵1<m<3,
∴1<k<2,
∴1<m<3符合题意;
③当3≤m≤5时,作投影矩形A′FB′E,如图7所示.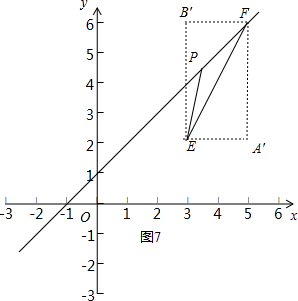
此时点E(3,2),FA′=6-2=4,FB′=5-3=2,△PEF的投影比k=$′\frac{FA′}{FB′}$=2,
∴3≤m≤5不符合题意;
④当m>5时,作投影矩形A′PB′E,如图8所示.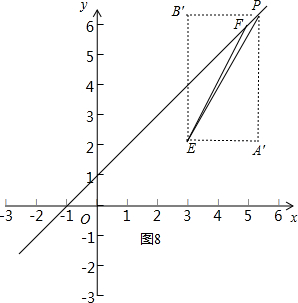
此时点P(m,m+1),点E(3,2),PB′=m+1-2=m-1,PA′=m-3,△PEF的投影比k=$\frac{PB′}{PA′}$=$\frac{m-1}{m-3}$,
∵m>5,
∴1<k<2,
∴m>5符合题意.
综上可知:点P的横坐标m的取值范围为1<m<3或m>5.
故答案为:1<m<3或m>5.
点评 本题考查了一次函数图象上点的坐标特征、矩形的性质以及解不等式,解题的关键是:(1)找出投影矩形的长边和短边长;(2)分两种情况考虑;(3)分四种情况考虑.本题属于中档题,难度不大,但解题过程中用到了分段考虑,给解题带来了麻烦,解决该题型题目时,画出图形,利用数形结合解决问题是关键.


科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,直线y1=mx与双曲线y2=$\frac{k}{x}$相交于点A、B,四边形AODC为菱形,点C在x轴正半轴上,点D的坐标为(2,-3).
如图,在平面直角坐标系中,直线y1=mx与双曲线y2=$\frac{k}{x}$相交于点A、B,四边形AODC为菱形,点C在x轴正半轴上,点D的坐标为(2,-3).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
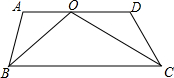 如图所示,AD∥BC,BO,CO分别平分∠ABC,∠DCB,若∠A+∠D=220°,则∠BOC的大小为( )
如图所示,AD∥BC,BO,CO分别平分∠ABC,∠DCB,若∠A+∠D=220°,则∠BOC的大小为( )| A. | 110° | B. | 120° | C. | 130° | D. | 140° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
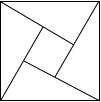 2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽的弦图,它是由四个全等的直角三角形和中间的小正方形拼成的大正方形,如图所示,如果大正方形的面积是13,小正方形的面积为1,直角三角形的较短直角边长为a,较长直角边长为b,那么(a+b)2的值为( )
2002年8月在北京召开的国际数学家大会会徽取材于我国古代数学家赵爽的弦图,它是由四个全等的直角三角形和中间的小正方形拼成的大正方形,如图所示,如果大正方形的面积是13,小正方形的面积为1,直角三角形的较短直角边长为a,较长直角边长为b,那么(a+b)2的值为( )| A. | 13 | B. | 19 | C. | 25 | D. | 169 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
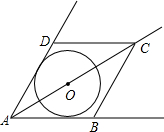 如图,菱形ABCD的边长为2,∠DAB=60°,点 O为射线AC上动点,动圆⊙O始终与射线AB相切,研究⊙O与菱形ABCD各边交点总个数的情况,以下论述正确的是( )
如图,菱形ABCD的边长为2,∠DAB=60°,点 O为射线AC上动点,动圆⊙O始终与射线AB相切,研究⊙O与菱形ABCD各边交点总个数的情况,以下论述正确的是( )| A. | ①②⑤ | B. | ② | C. | ①③④ | D. | ②④⑤ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com