
 如图,在平面直角坐标系中,直线y1=mx与双曲线y2=$\frac{k}{x}$相交于点A、B,四边形AODC为菱形,点C在x轴正半轴上,点D的坐标为(2,-3).
如图,在平面直角坐标系中,直线y1=mx与双曲线y2=$\frac{k}{x}$相交于点A、B,四边形AODC为菱形,点C在x轴正半轴上,点D的坐标为(2,-3).分析 (1)连接AD,交x轴于点E,根据菱形的性质结合点D的坐标可得出点A的坐标,结合点A的坐标利用待定系数法即可求出一次函数与反比例函数的关系式;
(2)根据函数的对称性结合点A的坐标可得出点B的坐标,由点A的坐标可得出点M的坐标,利用三角形的面积公式即可得出结论;
(3)根据两函数图象的上下位置关系结合交点的横坐标,即可得出不等式的解.
解答 解:(1)连接AD,交x轴于点E,如图1所示.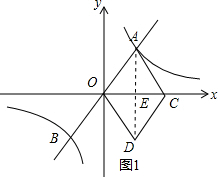
∵四边形AODC为菱形,
∴AD⊥OC,AE=DE.
∵点D的坐标为(2,-3),
∴点A的坐标为(2,3).
将点A(2,3)代入y1=mx中,
得:3=2m,解得:m=$\frac{3}{2}$,
∴一次函数的表达式为y1=$\frac{3}{2}$x.
将点A(2,3)代入y2=$\frac{k}{x}$中,
得:3=$\frac{k}{2}$,解得:k=6,
∴反比例函数表达式为y2=$\frac{6}{x}$.
(2)依照题意画出图形,如图2所示.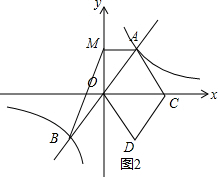
∵点A、点B关于点O成中心对称,且点A(2,3),
∴点B(-2,-3),点M(0,3),
∴AM=2.
S△ABM=$\frac{1}{2}$AM•(yA-yB)=$\frac{1}{2}$×2×[3-(-3)]=6.
(3)观察函数图象,发现:
当x<-2或0<x<2时,一次函数图象在反比例函数图象的下方,
∴不等式y1<y2的解为:x<-2或0<x<2.
故答案为:x<-2或0<x<2.
点评 本题考查了反比例函数与一次函数的交点问题、待定系数法求出函数解析式以及菱形的性质,解题的关键是:(1)利用待定系数法求出一次函数与反比例函数的解析式;(2)利用三角形的面积公式求出面积;(3)根据两函数图象的上下位置关系解不等式.本题属于中档题,难度不大,解决该题型题目时,找出点的坐标,利用待定系数法求出函数解析式是关键.


 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
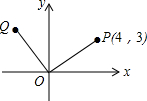 如图所示,点P的坐标为(4,3),把点P绕坐标原点O逆时针旋转90°后得到点Q.
如图所示,点P的坐标为(4,3),把点P绕坐标原点O逆时针旋转90°后得到点Q.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
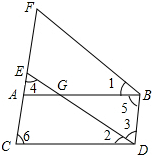 如图,∠1=∠2,∠3=∠4,∠5=∠6.求证:ED∥FB.在下面的括号中填上推理依据.
如图,∠1=∠2,∠3=∠4,∠5=∠6.求证:ED∥FB.在下面的括号中填上推理依据.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com