
【题目】如图,在南北方向的海岸线MN上,有A、B两艘巡逻船,现均收到故障船C的求救信号.已知A、B两船相距100(![]() +1)海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.
+1)海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.
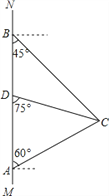
(1)分别求出A与C,A与D间的距离AC和AD(如果运算结果有根号,请保留根号).
(2)已知距离观测点D处100海里范围内有暗礁,若巡逻船A沿直线AC去营救船C,在去营救的途中有无触礁的危险?(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
【答案】 (1) AC之间的距离为200海里,AD的距离为200(![]() —1)海里;(2)无触礁危险。
—1)海里;(2)无触礁危险。
【解析】试题分析: (1)作CE⊥AB,设AE=x海里,则BE=CE=![]() x海里.根据AB=AE+BE=x+
x海里.根据AB=AE+BE=x+![]() x=100(
x=100(![]() +1),求得x的值后即可求得AC的长;过点D作DF⊥AC于点F,同理求出AD的长;
+1),求得x的值后即可求得AC的长;过点D作DF⊥AC于点F,同理求出AD的长;
(2)作DF⊥AC于点F,根据AD的长和∠DAF的度数求线段DF的长后与100比较即可得到答案.
试题解析:
(1)如图过C作CE⊥AB,
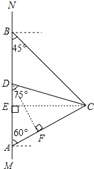
由题意得:∠ABC=45°,∠BAC=60°,
设AE=x海里,
在Rt△AEC中,CE=AEtan60°=![]() x;
x;
在Rt△BCE中,BE=CE=![]() x.
x.
∴AE+BE=x+![]() x=100(
x=100(![]() +1),
+1),
解得:x=100.
AC=2x=200.
在△ACD中,∠DAC=60°,∠ADC=75°,则∠ACD=45°.
过点D作DF⊥AC于点F,
设AF=y,则DF=CF=![]() y,
y,
∴AC=y+![]() y=200,
y=200,
解得:y=100(![]() 1),
1),
∴AD=2y=200(![]() 1).
1).
答:A与C之间的距离AC为200海里,A与D之间的距离AD为200(![]() 1)海里。
1)海里。
(2)由(1)可知,DF=![]() AF=
AF=![]() ×100(
×100(![]() 1)≈126.3海里,
1)≈126.3海里,
∵126.3>100,
所以巡逻船A沿直线AC航线,在去营救的途中没有触暗礁危险。


 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案科目:初中数学 来源: 题型:
【题目】学习了统计知识后,班主任王老师叫班长就本班同学的上学方式进行了一次调查统计,图1和图2是他通过收集数据后,绘制的两幅不完整的统计图,请你根据图中提供的信息,解答以下问题: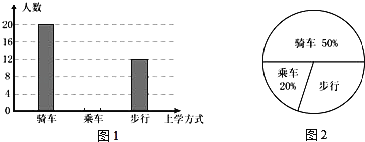
(1)在扇形统计图中,计算出“步行”部分所对应的圆心角的度数;
(2)求该班共有多少名学生;
(3)在图1中,将表示“乘车”的部分补充完整.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中正确的是( )
A.两条射线所组成的图形叫做角
B.一条直线可以看成一个平角
C.角的两边越长,角就越大
D.角的大小和它的度数大小是一致的
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AD是圆O的切线,切点为A,AB是圆O的弦。过点B作BC//AD,交圆O于点C,连接AC,过点C作CD//AB,交AD于点D。连接AO并延长交BC于点M,交过点C的直线于点P,且BCP=ACD。
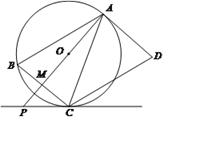
(1) 判断直线PC与圆O的位置关系,并说明理由:
(2) 若AB=9,BC=6,求PC的长。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c,且a>b>c,a+b+c=0,有以下四个命题,则一定正确命题的序号是( )
①x=1是二次方程ax2+bx+c=0的一个实数根;
②二次函数y=ax2+bx+c的开口向下;
③二次函数y=ax2+bx+c的对称轴在y轴的左侧;
④不等式4a+2b+c>0一定成立.
A. ①② B. ①③ C. ①④ D. ③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知a,b,c是三角形的三条边,则|a+b﹣c|﹣|c﹣a﹣b|的化简结果为( )
A. 0 B. 2a+2b C. 2c D. 2a+2b﹣2c
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,过反比例函数y= ![]() (x>0)的图象上任意两点A、B分别作x轴的垂线,垂足分别为C、D,连接OA、OB,设AC与OB的交点为E,△AOE与梯形ECDB的面积分别为S1、S2 , 比较它们的大小,可得( )
(x>0)的图象上任意两点A、B分别作x轴的垂线,垂足分别为C、D,连接OA、OB,设AC与OB的交点为E,△AOE与梯形ECDB的面积分别为S1、S2 , 比较它们的大小,可得( ) 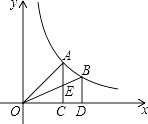
A.S1>S2
B.S1=S2
C.Sl<S2
D.大小关系不能确定
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com