
【题目】如图,AD是圆O的切线,切点为A,AB是圆O的弦。过点B作BC//AD,交圆O于点C,连接AC,过点C作CD//AB,交AD于点D。连接AO并延长交BC于点M,交过点C的直线于点P,且BCP=ACD。
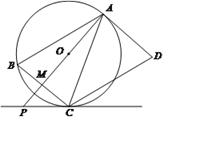
(1) 判断直线PC与圆O的位置关系,并说明理由:
(2) 若AB=9,BC=6,求PC的长。
【答案】(1)相切;证明见解析;(2)![]() .
.
【解析】试题分析:(1)通过分析,直线与圆O已经有一个公共点,连接半径0C,只要证明OC⊥PC即可;(2)根据AD是切线和AD∥BC证明AP⊥BC,利用垂径定理计算出CM=BM=3,在Rt△AMB中,利用勾股定义计算出AM的长,在Rt△OMC中,利用勾股定理建立方程计算出圆O的半径的长,最后证明△OMC~△OCP,利用相似三角形的对应边成比例计算出PC的长.
试题解析:(1) 直线PC与圆O相切.
连接CO并延长,交圆O于点N,连接BN.
∵AB//CD,
∴BAC=ACD.
∵BAC=BNC,
∴BNC=ACD.
∵BCP=ACD,
∴BNC=BCP.
∵CN是圆O的直径,
∴CBN=90°.
∴BNC+BCN=90°,
∴BCP+BCN=90°.
∴PCO=90°,即PC^OC.
又∵点C在圆O上,
∴直线PC与圆O相切.
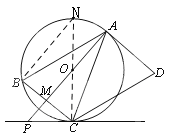
(2) ∵AD是圆O的切线,
∴AD^OA,即OAD=90°.
∵BC//AD,
∴OMC=180°-OAD=90°,即OM^BC.
∴MC=MB.
∴AB=AC.
在Rt△AMC中,AMC=90°,AC=AB=9,MC=![]() BC=3,
BC=3,
由勾股定理,得AM=![]() =
=![]() =6
=6![]() .
.
设圆O的半径为r.
在Rt△OMC中,OMC=90°,OM=AM-AO=6![]() -r,MC=3,OC=r,
-r,MC=3,OC=r,
由勾股定理,得OM 2+MC 2=OC 2,
∴(6![]() -r)2+32=r2.
-r)2+32=r2.
解得r=![]() .
.
在△OMC和△OCP中,
∵OMC=OCP,MOC=COP,
∴△OMC~△OCP.
∴![]() =
=![]() ,即
,即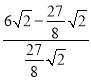 =
=![]() .
.
∴PC=![]() .
.


科目:初中数学 来源: 题型:
【题目】某市甲、乙两个汽车销售公司,去年一至十月份每月销售同种品牌汽车的情况如图所示: 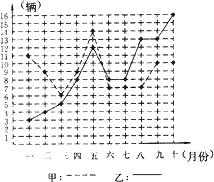
(1)请你根据上图填写下表:
销售公司 | 平均数 | 方差 | 中位数 | 众数 |
甲 | 5.2 | 9 | ||
乙 | 9 | 17.0 | 8 |
(2)请你从以下两个不同的方面对甲、乙两个汽车销售公司去年一至十月份的销售情况进行分析: ①从平均数和方差结合看;
②从折线图上甲、乙两个汽车销售公司销售数量的趋势看(分析哪个汽车销售公司较有潜力).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系XOY中,有A(3,2),B (﹣1,﹣4 ),P是X轴上的一点,Q是Y轴上的一点,若以点A,B,P,Q四个点为顶点的四边形是平行四边形,则Q点的坐标是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在南北方向的海岸线MN上,有A、B两艘巡逻船,现均收到故障船C的求救信号.已知A、B两船相距100(![]() +1)海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.
+1)海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.
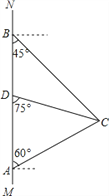
(1)分别求出A与C,A与D间的距离AC和AD(如果运算结果有根号,请保留根号).
(2)已知距离观测点D处100海里范围内有暗礁,若巡逻船A沿直线AC去营救船C,在去营救的途中有无触礁的危险?(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水果店王阿姨到水果批发市场打算购进一种水果销售,经过还价,实际价格每千克比原来少2元,发现原来买这种80千克的钱,现在可买88千克。
(1)现在实际这种每千克多少元?
(2)准备这种,若这种的量y(千克)与单价x(元/千克)满足如图所示的一次函数关系。
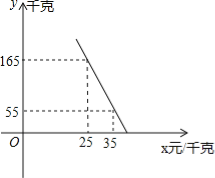
①求y与x之间的函数关系式;
②请你帮拿个主意,将这种的单价定为多少时,能获得最大利润?最大利润是多少?(利润=收入-进货金额)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,将抛物线y=2(x﹣1)2+1先向左平移2个单位,再向上平移3个单位,则平移后抛物线的表达式是( )
A.y=2(x+1)2+4B.y=2(x﹣1)2+4
C.y=2(x+2)2+4D.y=2(x﹣3)2+4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列诗句表述的是随机事件的是( )
A.离离原上草,一岁一枯荣B.危楼高百尺,手可摘星辰
C.会当凌绝顶,一览众山小D.东边日出西边雨,道是无晴却有晴
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com