
【题目】某网店尝试用单价随天数而变化的销售模式销售一种商品,利用30天的时间销售一种成本为10元/件的商品售后,经过统计得到此商品单价在第x天(x为正整数)销售的相关信息:销售量![]() (单位:件),销售单价m(元/件)
(单位:件),销售单价m(元/件)
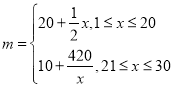
(1)请计算第几天该商品单价为25元/件?
(2)求网店销售该商品30天里所获利润y(元)关于x(天)的函数关系式;
(3)这30天中第几天获得的利润最大?最大利润是多少?
【答案】(1)第10天或第28天时该商品为25元/件;
(2)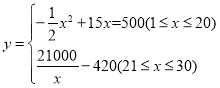 ;
;
(3)第15天时获得利润最大,最大利润为612.5元.
【解析】
试题(1)分两种情形分别代入解方程即可.(2)分两种情形写出所获利润y(元)关于x(天)的函数关系式即可.(3)分两种情形根据函数的性质解决问题即可.
试题解析:(1)分两种情况:
①当1≤x≤20时,将m=25代入m=20+![]() x,解得x=10
x,解得x=10
②当21≤x≤30时,25=10+![]() ,解得x=28
,解得x=28
经检验x=28是方程的解
∴x=28
答:第10天或第28天时该商品为25元/件.
(2)分两种情况
①当1≤x≤20时,y=(m﹣10)n=(20+![]() x﹣10)(50﹣x)=﹣
x﹣10)(50﹣x)=﹣![]() x2+15x+500,
x2+15x+500,
②当21≤x≤30时,y=(10+![]() ﹣10)(50﹣x)=
﹣10)(50﹣x)=![]()
综上所述: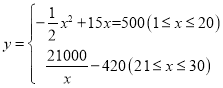
(3)①当1≤x≤20时
由y=﹣![]() x2+15x+500=﹣
x2+15x+500=﹣![]() (x﹣15)2+
(x﹣15)2+![]() ,∵a=﹣
,∵a=﹣![]() <0,
<0,
∴当x=15时,y最大值=![]() .
.
②当21≤x≤30时,由y=![]() ﹣420,可知y随x的增大而减小
﹣420,可知y随x的增大而减小
∴当x=21时,y最大值=![]() ﹣420=580元.
﹣420=580元.
∵580<![]()
∴第15天时获得利润最大,最大利润为612.5元.


 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,若△ABC内一点P满足∠PAC=∠PCB=∠PBA,则称点P为△ABC的布罗卡尔点,已知△ABC中,CA=CB,∠ACB=120°,P为△ABC的布罗卡尔点,若![]() ,则PB+PC=_____.
,则PB+PC=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为建设资源节约型、环境友好型社会,克服因干旱而造成的电力紧张困难,切实做好节能减排工作.某地决定对居民家庭用电实行“阶梯电价”,电力公司规定:居民家庭每月用电量在80千瓦时以下(含80千瓦时,1千瓦时俗称1度)时,实行“基本电价”;当居民家庭月用电量超过80千瓦时时,超过部分实行“提高电价”.
(1)小张家今年2月份用电100千瓦时,上缴电费68元;5月份用电120千瓦时,上缴电费88元.求“基本电价”和“提高电价”分别为多少元/千瓦时;
(2)若6月份小张家预计用电130千瓦时,请预算小张家6月份应上缴的电费.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数的图象经过A(2,0)、C(0,12) 两点,且对称轴为直线x=4. 设顶点为点P,与x轴的另一交点为点B.
(1)求二次函数的解析式及顶点P的坐标;
(2)如图,在直线 y=2x上是否存在点D,使四边形OPBD为等腰梯形?若存在,求出点D的坐标;若不存在,请说明理由;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知二次函数y=ax2+bx+c的图象过A(2,0),B(0,﹣1)和C(4,5)三点.
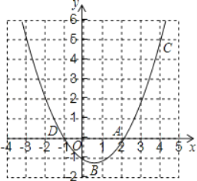
(1)求二次函数的解析式;
(2)设二次函数的图象与x轴的另一个交点为D,求点D的坐标;
(3)在同一坐标系中画出直线y=x+1,并写出当x在什么范围内时,一次函数的值大于二次函数的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径为AB,点C在圆周上(异于A,B),AD⊥CD.
(1)若BC=3,AB=5,求AC的值;
(2)若AC是∠DAB的平分线,求证:直线CD是⊙O的切线.
查看答案和解析>>
科目:初中数学 来源: 题型:
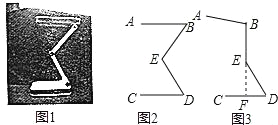
【题目】图1是一种可折叠台灯,它放置在水平桌面上,将其抽象成图2,其中点B,E,D均为可转动点.现测得AB=BE=ED=CD=15cm,经多次调试发现当点B,E所在直线垂直经过CD的中点F时(如图3所示)放置较平稳.
(1)求平稳放置时灯座DC与灯杆DE的夹角的大小;
(2)为保护视力,写字时眼睛离桌面的距离应保持在30cm,为防止台灯刺眼,点A离桌面的距离应不超过30cm,求台灯平稳放置时∠ABE的最大值.(结果精确到0.01°,参考数据: ![]() ≈1.732,sin7.70°≈0.134,cos82.30°≈0.134,可使用科学计算器)
≈1.732,sin7.70°≈0.134,cos82.30°≈0.134,可使用科学计算器)
查看答案和解析>>
科目:初中数学 来源: 题型:
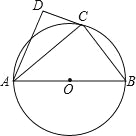
【题目】如图,⊙O是△ABC的外接圆,AB是⊙O的直径,D为⊙O上一点,OD⊥AC,垂足为E,连接BD.

(1)求证:BD平分∠ABC;
(2) 当∠ODB=30°时,求证:BC=OD.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com