
【题目】如图,在![]() 中,
中,![]() 是
是![]() 内两点,
内两点,![]() 平分
平分![]()
![]() ,若
,若![]() ,
,![]() ,则
,则![]() ____________
____________![]() .
.
【答案】12
【解析】
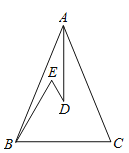
首先延长ED交BC于M,延长AD交BC于N,过点D作DF∥BC,交BE于F,易得:△EFD∽△EBM,又由AB=AC,AD平分∠BAC,根据等腰三角形的性质,即可得AN⊥BC,BN=CN,又由∠EBC=∠E=60°,可得△BEM与△EFD为等边三角形,又由直角三角形中,30°角所对的直角边是斜边的一半,即可求得MN与BM的值,继而求得答案.
解:延长ED交BC于M,延长AD交BC于N,过点D作DF∥BC,交BE于F,
∴△EFD∽△EBM,
∵AB=AC,AD平分∠BAC,
∴AN⊥BC,BN=CN,
∵∠EBC=∠E=60°,
∴△BEM为等边三角形,
∴△EFD为等边三角形,
∵BE=9cm,DE=3cm,
∴DM=6cm,
∵∠DNM=90°,∠DMN=60°,
∴∠NDM=30°,
∴NM=![]() DM=3cm,
DM=3cm,
∴BN=BM-MN=9-3=6(cm),
∴BC=2BN=12(cm).


科目:初中数学 来源: 题型:
【题目】在图1,2,3中,已知![]() ,
,![]() ,点
,点![]() 为线段
为线段![]() 上的动点,连接
上的动点,连接![]() ,以
,以![]() 为边向上作菱形
为边向上作菱形![]() ,且
,且![]() .
.
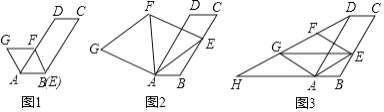
(1)如图1,当点![]() 与点
与点![]() 重合时,
重合时,![]() ________°;
________°;
(2)如图2,连接![]() .
.
①填空:![]() _________
_________![]() (填“>”,“<”,“=”);
(填“>”,“<”,“=”);
②求证:点![]() 在
在![]() 的平分线上;
的平分线上;
(3)如图3,连接![]() ,
,![]() ,并延长
,并延长![]() 交
交![]() 的延长线于点
的延长线于点![]() ,当四边形
,当四边形![]() 是平行四边形时,求
是平行四边形时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组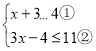
请结合题意填空,完成本题的解答:
(I)解不等式①,得_____________________;
(Ⅱ)解不等式②,得_________________________;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:

(IV)原不等式组的解集为____________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数![]() 的图象,其对称轴为
的图象,其对称轴为![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④若
;④若![]() 是抛物线上两点,则
是抛物线上两点,则![]() .其中正确的结论有( )
.其中正确的结论有( )
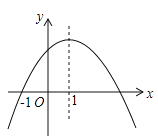
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组 ;请结合题意填空,完成本题的解答.
;请结合题意填空,完成本题的解答.
(Ⅰ)解不等式①,得 ;
(Ⅱ)解不等式②,得 ;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:
![]()
(Ⅳ)原不等式组的解集为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
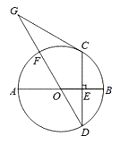
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点E,点G在直径DF的延长线上,∠D=∠G=30°.
(1)求证:CG是⊙O的切线 (2)若CD=6,求GF的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某网店尝试用单价随天数而变化的销售模式销售一种商品,利用30天的时间销售一种成本为10元/件的商品售后,经过统计得到此商品单价在第x天(x为正整数)销售的相关信息:销售量![]() (单位:件),销售单价m(元/件)
(单位:件),销售单价m(元/件)
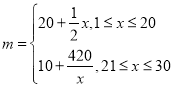
(1)请计算第几天该商品单价为25元/件?
(2)求网店销售该商品30天里所获利润y(元)关于x(天)的函数关系式;
(3)这30天中第几天获得的利润最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,已知BC=6,BC边上中线AD=5.点P为线段AD上一点(与点A、D不重合),过P点作EF∥BC,分别交边AB、AC于点E、F,过点E、F分别作EG∥AD,FH∥AD,交BC边于点G、H.
(1)求证:P是线段EF的中点;
(2)当四边形EGHF为菱形时,求EF的长;
(3) 如果sin∠ADC=![]() ,设AP长为x,四边形EGHF面积为y,求y关于x的函数解析式及其定义域.
,设AP长为x,四边形EGHF面积为y,求y关于x的函数解析式及其定义域.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com