
【题目】如图是二次函数![]() 的图象,其对称轴为
的图象,其对称轴为![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④若
;④若![]() 是抛物线上两点,则
是抛物线上两点,则![]() .其中正确的结论有( )
.其中正确的结论有( )
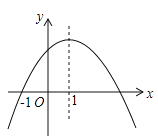
A. 1个B. 2个C. 3个D. 4个
【答案】B
【解析】
由抛物线开口方向得到a<0,根据对称轴得到b=-2a>0,由抛物线与y轴的交点位置得到c>0,则可对①进行判断;由b=-2a可对②进行判断;利用抛物线的对称性可得到抛物线与x轴的另一个交点为(3,0),则可判断当x=3时,y=0,于是可对③进行判断;通过二次函数的增减性可对④进行判断.
解:∵抛物线开口向下,
∴a<0,
∵抛物线的对称轴为直线![]() ,∴b=-2a>0,
,∴b=-2a>0,
∵抛物线与y轴的交点在x轴上方,
∴c>0,
∴abc<0,所以①错误;
∵b=-2a,
∴2a+b=0,所以②正确;
∵抛物线与x轴的一个交点为(-1,0),抛物线的对称轴为直线x=1,
∴抛物线与x轴的另一个交点为(3,0),
∴当x=3时,y=0,
∴![]() ,所以③错误;
,所以③错误;
∵抛物线的对称轴为直线x=1,且抛物线开口向下,
∴当x![]() 时,y随x的增大而增大
时,y随x的增大而增大
∵![]()
点![]() 到对称轴的距离比点
到对称轴的距离比点![]() 对称轴的距离近,
对称轴的距离近,
∴y1![]() y2,所以④正确.
y2,所以④正确.
故选:B.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】为纪念建国70周年,某校举行班级歌咏比赛,歌曲有:《我爱你,中国》,《歌唱祖国》,《我和我的祖国》(分别用字母A,B,C依次表示这三首歌曲).比赛时,将A,B,C这三个字母分别写在3张无差别不透明的卡片正面上,洗匀后正面向下放在桌面上,八(1)班班长先从中随机抽取一张卡片,放回后洗匀,再由八(2)班班长从中随机抽取一张卡片,进行歌咏比赛.
(1)八(1)班抽中歌曲《我和我的祖国》的概率是__________;
(2)试用画树状图或列表的方法表示所有可能的结果,并求出八(1)班和八(2)班抽中不同歌曲的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=x+m与双曲线y=![]() 相交于A(2,1),B两点.
相交于A(2,1),B两点.
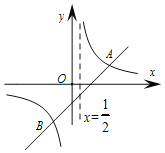
(1)求出一次函数与反比例函数的解析式,并求出B点坐标;
(2)若P为直线x=![]() 上一点,当△APB的面积为6时,请求出点P的坐标.
上一点,当△APB的面积为6时,请求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
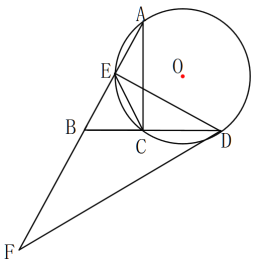
【题目】如图,在 RtABC 中,ACB 90 ,点 E 为 AB 中点,经过 A 、C 、E 三点的⊙O 与 BC的延长线相交于点 D ,过点 D 的直线交 AB 的延长线于点 F ,且FDB CED 。
(1)求证: DF 为⊙O 的切线;
(2)若 AE ![]() ,CD 1,求 DF ;
,CD 1,求 DF ;
(3)若 BF mBE ,求sin BAC (用含 m 的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组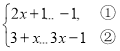
请结合题意填空,完成本题的解答。
(I)解不等式①,得________________
(Ⅱ)解不等式②,得:_____________________
(Ⅲ)把不等式①和②的解集在数轴上表示出来:

(IV)原不等式组的解集为___________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,解答问题
(2x﹣5)2+(3x+7)2=(5x+2)2
解:设m=2x﹣5,n=3x+7,则m+n=5x+2
则原方程可化为m2+n2=(m+n)2
所以mn=0,即(2x﹣5)(3x+7)=0
解之得,x1=![]() ,x2=﹣
,x2=﹣![]()
请利用上述方法解方程(4x﹣5)2+(3x﹣2)2=(x﹣3)2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数的图象经过A(2,0)、C(0,12) 两点,且对称轴为直线x=4. 设顶点为点P,与x轴的另一交点为点B.
(1)求二次函数的解析式及顶点P的坐标;
(2)如图,在直线 y=2x上是否存在点D,使四边形OPBD为等腰梯形?若存在,求出点D的坐标;若不存在,请说明理由;

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】P是△ABC一边上的一点(P不与A、B、C重合),过点P的一条直线截△ABC,如果截得的三角形与△ABC相似,我们称这条直线为过点P的△ABC的“相似线”.Rt△ABC中,∠C=90°,∠A=30°,当点P为AC的中点时,过点P的△ABC的“相似线”最多有几条?( )
A. 1条B. 2条C. 3条D. 4条
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com