
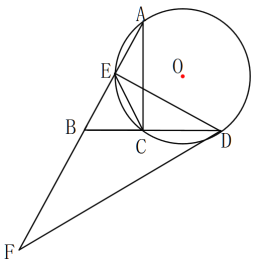
【题目】如图,在 RtABC 中,ACB 90 ,点 E 为 AB 中点,经过 A 、C 、E 三点的⊙O 与 BC的延长线相交于点 D ,过点 D 的直线交 AB 的延长线于点 F ,且FDB CED 。
(1)求证: DF 为⊙O 的切线;
(2)若 AE ![]() ,CD 1,求 DF ;
,CD 1,求 DF ;
(3)若 BF mBE ,求sin BAC (用含 m 的代数式表示).
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)连接AD,由圆周角定理可得到∠CED=∠CAD,进而证得∠CAD=∠FDB, ∠ADF=90°,所以得到DF 为⊙O 的切线;
(2)先证得AD=BD,再设BC=x,则BD=1+x=AD,根据勾股定理列出![]() 解得x=3, AD=4,再求得
解得x=3, AD=4,再求得![]() ,再证得∠ADE=∠F并根据它们的正切值相等列出方程,
,再证得∠ADE=∠F并根据它们的正切值相等列出方程,![]() 即可求出DF;
即可求出DF;
(3)设BE=a,则BF=ma,AE=a,AF=(m+2)a,EF=(m+1)a,由射影定理可证![]() ,
,![]() ,
,![]() ,再证得∠ADE=∠BDE=∠BAC=∠F,则
,再证得∠ADE=∠BDE=∠BAC=∠F,则![]()
(1)连接AD
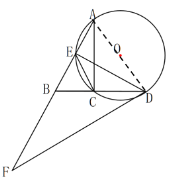
∵∠ACD=90°,
∴∠CAD+∠ADC=90°,AD是直径.
∵∠CED=∠CAD, ∠CED=∠FDB,
∴∠CAD=∠FDB,
∴∠ADC+∠FDB=90°,即∠ADF=90°,
∴DF 为⊙O 的切线;
(2) ∵∠ACD=90°,
∴AD是直径,
∴DE⊥AB,
∵点 E 为 AB 中点,
∴DE是AB的中垂线,
∴AD=BD
设BC=x,则BD=1+x=AD,
在Rt△ABC中,![]()
Rt△ACD中,![]()
∴![]()
解得![]() (舍去),
(舍去),
∴AD=4
在Rt△ADE中,![]() ,
,
由已知易证∠ADE=∠F
∴![]()
![]()
∴![]()
![]()
(3)设BE=a,则BF=ma,
AE=a,AF=(m+2)a,EF=(m+1)a
在Rt△ADF中,由射影定理可证![]()
![]()
![]()

∵∠ADF=90°,DE垂直平分AB, ∠ACD=90°,
∴∠ADE=∠BDE=∠BAC=∠F,
∴![]()


 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:初中数学 来源: 题型:
【题目】某市开展“美丽家乡,创卫同行”活动,某校倡议学生利用双休日参加义务劳动,为了解同学们劳动情况,学校随机调查了部分同学的劳动时间,并用得到的数据绘制了不完整的统计图①和图②,请根据相关信息,解答下列问题:
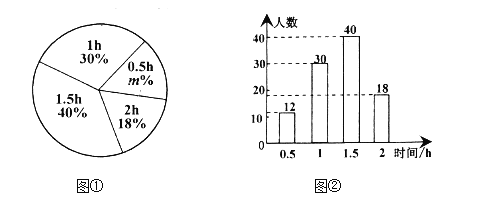
(Ⅰ)本次接受随机抽样调查的学生人数为 ,图①中![]() 的值是 ;
的值是 ;
(Ⅱ)求本次调查获取的样本数据的平均数、众数和中位数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】居民区内的“广场舞”引起媒体关注,小王想了解本小区居民对“广场舞”的看法,进行一次分四个层次的抽样调查(四个层次为:A,非常赞同;B.赞同但要有时间限制;C.无所谓;D.不赞同),并把调查结果绘制成如下两幅不完整的统计图,请根据统计图中的倍息解答下列问题:

(1)本次被抽查的居民人数是 人,将条形统计图补充完整.
(2)图中∠α的度数是 度;该小区有3000名居民,请估计对“广场舞”表示赞同(包括A层次和B层次)的大约有人
(3)据了解,甲、乙、丙、丁四位居民投不赞同票,小王想从这四位居民中随机选择两位了解具体情况,请用列表或画树状图的方法求出恰好选中甲和乙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组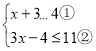
请结合题意填空,完成本题的解答:
(I)解不等式①,得_____________________;
(Ⅱ)解不等式②,得_________________________;
(Ⅲ)把不等式①和②的解集在数轴上表示出来:

(IV)原不等式组的解集为____________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
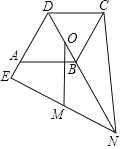
【题目】已知菱形 ABCD 中, ADC 120 , F 为 DB 延长线上一点, E 为 DA 延长线上一点, 且 BF DE , 连 CF 、 EF , 点 O 为 BD 的中点, 过 O 作 OM AB 交 EF 于 M , 若OM ![]() ,AE 1,则 AB 的长度为( )
,AE 1,则 AB 的长度为( )
A.![]() B.2C.
B.2C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是二次函数![]() 的图象,其对称轴为
的图象,其对称轴为![]() .下列结论:①
.下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④若
;④若![]() 是抛物线上两点,则
是抛物线上两点,则![]() .其中正确的结论有( )
.其中正确的结论有( )
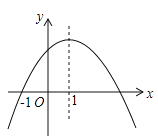
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
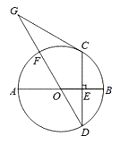
【题目】如图,AB是⊙O的直径,弦CD⊥AB于点E,点G在直径DF的延长线上,∠D=∠G=30°.
(1)求证:CG是⊙O的切线 (2)若CD=6,求GF的长
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com