
����Ŀ���������ڵġ��㳡�衱����ý���ע��С�����˽ⱾС������ԡ��㳡�衱�Ŀ���������һ�η��ĸ���εij������飨�ĸ����Ϊ��A���dz���ͬ��B����ͬ��Ҫ��ʱ�����ƣ�C������ν��D������ͬ�������ѵ��������Ƴ�����������������ͳ��ͼ�������ͳ��ͼ�еı�Ϣ����������⣺

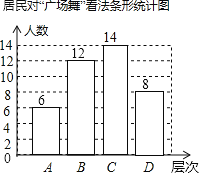
��1�����α����ľ����������� ���ˣ�������ͳ��ͼ����������
��2��ͼ�С����Ķ������� ���ȣ���С����3000����������ƶԡ��㳡�衱��ʾ��ͬ������A��κ�B��Σ��Ĵ�Լ����
��3�����˽⣬�ס��ҡ���������λ����Ͷ����ͬƱ��С���������λ���������ѡ����λ�˽��������������б�����״ͼ�ķ������ǡ��ѡ�м��ҵĸ��ʣ�
���𰸡���1��40������������2��54���ԡ��㳡�衱��ʾ��ͬ������A��κ�B��Σ��Ĵ�Լ��1350�ˣ���3����������![]() ��
��
��������
��1����A��ε�������������ռ�İٷֱȵõ���������������ټ����C��ε�������Ȼ��ȫ����ͳ��ͼ��
��2����A��ε�������ռ�İٷֱȳ���360��õ������Ķ�������3000�ֱ����������A��B��ε�������ռ�İٷֱȣ������ǵĺͿɹ��Ƴ�С���ԡ��㳡�衱��ʾ��ͬ������A��κ�B��Σ���������
��3������״ͼչʾ����12�ֵȿ��ܵĽ�������ҳ�ǡ��ѡ�м��ҵĽ������Ȼ����ݸ��ʹ�ʽ��⣮
�⣺��1��12��30%��40��
���Ա��α����ľ���������40�ˣ�
C��ε�����Ϊ40��6��12��8��14���ˣ���
����ͳ��ͼ����Ϊ��
��2��������360���![]() ��54�㣬
��54�㣬
3000��![]() ��1350��
��1350��
���Թ��ƶԡ��㳡�衱��ʾ��ͬ������A��κ�B��Σ��Ĵ�Լ��1350�ˣ�
�ʴ�Ϊ40��54��
��3������״ͼΪ��

����12�ֵȿ��ܵĽ����������ǡ��ѡ�м��ҵĽ����Ϊ2��
����ǡ��ѡ�м��ҵĸ��ʣ�![]() ��
��![]() ��
��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A��B������ֱ�ΪA��0��a����B��b��a������a��b���㣨a��3��2+|b��6|��0����ͬʱ����A��B�ֱ�����ƽ��3����λ��������ƽ��2����λ���ֱ�õ���A��B�Ķ�Ӧ��C��D������AC��BD��AB��

��1�����C��D�����꼰�ı���ABDC�����S�ı���ABCD��
��2����y�����Ƿ����һ��M������MC��MD��ʹS��MCD��![]() S�ı���ABCD������������һ�㣬�����M�����꣬�������ڣ���˵�����ɣ�
S�ı���ABCD������������һ�㣬�����M�����꣬�������ڣ���˵�����ɣ�
��3����P��ֱ��BD�ϵ�һ�����㣬����PA��PO������P��BD���ƶ�ʱ������B��D�غϣ���ֱ��д����BAP����DOP����APO֮�������������ϵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�����70���꣬ijУ���а༶��ӽ�����������У����Ұ��㣬�й��������質����������Һ��ҵ���������ֱ�����ĸA��B��C���α�ʾ����������������ʱ����A��B��C��������ĸ�ֱ�д��3��������Ŀ�Ƭ�����ϣ�ϴ�Ⱥ��������·��������ϣ��ˣ�1�����ȴ��������ȡһ�ſ�Ƭ���Żغ�ϴ�ȣ����ɰˣ�2�������������ȡһ�ſ�Ƭ�����и�ӽ������
��1���ˣ�1������и������Һ��ҵ�������ĸ�����__________��
��2�����û���״ͼ���б��ķ�����ʾ���п��ܵĽ����������ˣ�1����Ͱˣ�2������в�ͬ�����ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ÿ��С�����εı߳�Ϊ1�������У���![]() ���ڸ���ϡ�
���ڸ���ϡ�

����AC�ij���_____________��
�����ı���![]() �۵���ʹ��C���4�غϣ��ۺ�EF��BC�ڵ�E����AD�ڵ�F����D�Ķ�Ӧ��ΪQ���������
�۵���ʹ��C���4�غϣ��ۺ�EF��BC�ڵ�E����AD�ڵ�F����D�Ķ�Ӧ��ΪQ���������![]() .�����̶ȵ�ֱ���������л����۵��������Σ�����Ҫ˵����
.�����̶ȵ�ֱ���������л����۵��������Σ�����Ҫ˵����![]() ��λ��������ҵ���____________________.
��λ��������ҵ���____________________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��A��B�Ƿ���������y��![]() ��x��0��ͼ���ϵ����㣬�ֱ��A��B������x�ᣬy�������߶Σ�AD��BE�����߶ν��ڵ�G����ͼ����Ӱ���ֵ����Ϊ3�����OAB�����Ϊ��������
��x��0��ͼ���ϵ����㣬�ֱ��A��B������x�ᣬy�������߶Σ�AD��BE�����߶ν��ڵ�G����ͼ����Ӱ���ֵ����Ϊ3�����OAB�����Ϊ��������
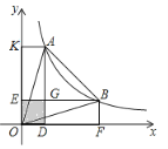
A.9B.10C.11D.12
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC��һ��P�����PAC����PCB����PBA����Ƶ�PΪ��ABC�IJ������㣬��֪��ABC�У�CA��CB����ACB��120�㣬PΪ��ABC�IJ������㣬��![]() ����PB+PC��_____��
����PB+PC��_____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y��x+m��˫����y��![]() �ཻ��A��2��1����B���㣮
�ཻ��A��2��1����B���㣮
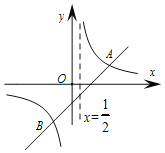
��1�����һ�κ����뷴���������Ľ���ʽ�������B�����ꣻ
��2����PΪֱ��x��![]() ��һ�㣬����APB�����Ϊ6ʱ���������P�����꣮
��һ�㣬����APB�����Ϊ6ʱ���������P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
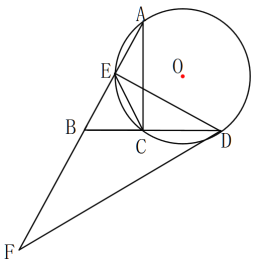
����Ŀ����ͼ���� RtABC �У�ACB 90 ���� E Ϊ AB �е㣬���� A ��C ��E ����ġ�O �� BC���ӳ����ཻ�ڵ� D ������ D ��ֱ�߽� AB ���ӳ����ڵ� F ����FDB CED ��
��1����֤�� DF Ϊ��O �����ߣ�
��2���� AE ![]() ��CD 1���� DF ��
��CD 1���� DF ��
��3���� BF mBE ����sin BAC ���ú� m �Ĵ���ʽ��ʾ��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ�����ͼ��A��2��0����C(0��12) ���㣬�ҶԳ���Ϊֱ��x=4. �趥��Ϊ��P����x�����һ����Ϊ��B.
��1������κ����Ľ���ʽ������P�����ꣻ
��2����ͼ����ֱ�� y=2x���Ƿ���ڵ�D��ʹ�ı���OPBDΪ�������Σ������ڣ������D�����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com