
【题目】如图,A,B是反比例函数y=![]() (x>0)图象上的两点,分别过A,B两点向x轴,y轴作垂线段,AD,BE两垂线段交于点G.若图中阴影部分的面积为3,则△OAB的面积为( )
(x>0)图象上的两点,分别过A,B两点向x轴,y轴作垂线段,AD,BE两垂线段交于点G.若图中阴影部分的面积为3,则△OAB的面积为( )
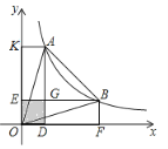
A.9B.10C.11D.12
【答案】D
【解析】
首先根据反比例函数图象上的点与坐标轴、向坐标轴作垂线所围成的矩形面积等于|k|,利用阴影部分的面积为3,推导出线段比例关系,比例关系转化为求矩形OFPK的面积,用割补法可求△OAB的面积.
解: 
设FB与KA的延长线相交于点P,
HM垂直平分EK,
∵A,B是反比例函数y=![]() (x>0)图象上的两点,
(x>0)图象上的两点,
A点向x轴,y轴作垂线段分别是AD、AK
∴s矩形ODAK=|k|=9
同理:s矩形OFBE=9
∵s矩形ODGE=3
∴s矩形DFBG=s矩形EGAK=9﹣3=6
∵HM垂直平分EK
∴OE=EH=HK
∴s矩形OFPK=3s矩形OFBE=3×9=27
且s矩形AGBP=2s△ABP=12
即s△ABP=6
∴s△AOB=S矩OFPK-S△AOK -S△OFB-S△ABP=27﹣6﹣9=12
故选:D.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
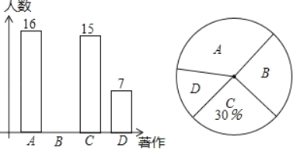
【题目】某校对A《唐诗》、B《宋词》、C《蒙山童韵》、D其它,这四类著作开展“最受欢迎的传统文化著作”调查,随机调查了若干名学生(每名学生必选且只能选这四类著作中的一种)并将得到的信息绘制了下面两幅不完整的统计图:
(1)求一共调查了多少名学生;
(2)请将条形统计图补充完整;
(3)该校语文老师想从这四类著作中随机选取两类作为学生寒假必读书籍,请用树状图或列表的方法求恰好选中《宋词》和《蒙山童韵》的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程ax2+bx+c=0的两实数根为x1,x2,根据一元二次方程解的意义和因式分解法解一元二次方程可知,x1,x2也是(x﹣x1)(x﹣x2)=0的两个实数根,所以ax2+bx+c=a(x﹣x1)(x﹣x2).
利用这个结论可以解决一些相关问题.
(1)实数范围内因式分解:
例:分解因式2x2+2x﹣1
解:令2x2+2x﹣1=0,解这个方程,得
![]() =
=![]() .
.
即x1=![]() ,x2=
,x2=![]() .
.
所以 2x2+2x﹣1=![]() .
.
试仿照上例在实数范围内分解因式:x2﹣6x+1;
(2)解不等式:x2+2x﹣1>0;
(3)灵活运用:
已知方程(x﹣a)(x﹣b)﹣x=0的两个实数根是c、d,求方程(2x﹣c)(2x﹣d)+2x=0的根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() 的顶点坐标分别为
的顶点坐标分别为![]() ,
,![]() ,
,![]() .动点
.动点![]() ,
,![]() 同时从点
同时从点![]() 出发,
出发,![]() 沿
沿![]() ,
,![]() 沿折线
沿折线![]() ,均以每秒1个单位长度的速度移动,当一个动点到达终点
,均以每秒1个单位长度的速度移动,当一个动点到达终点![]() 时,另一个动点也随之停止移动,移动时间记为
时,另一个动点也随之停止移动,移动时间记为![]() 秒,连接
秒,连接![]() .
.
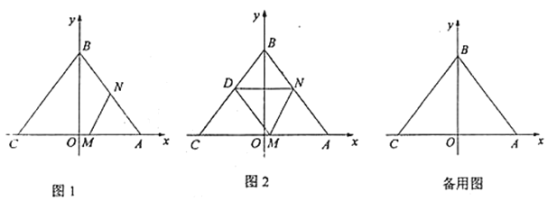
(Ⅰ)如图1,当点![]() 移动到
移动到![]() 中点时,求此时
中点时,求此时![]() 的值及
的值及![]() 点坐标;
点坐标;
(Ⅱ)在移动过程中,将![]() 沿直线
沿直线![]() 翻折,点
翻折,点![]() 的对称点为
的对称点为![]() .
.
①如图2,当点![]() 恰好落在
恰好落在![]() 边上的点
边上的点![]() 处时,求此时
处时,求此时![]() 的值;
的值;
②当点![]() 移动到点
移动到点![]() 时,点
时,点![]() 落在点
落在点![]() 处,求此时点
处,求此时点![]() 的坐标(直接写出结果即可).
的坐标(直接写出结果即可).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】3月12日是我国义务植树节。某校组织学生开展义务植树活动,在活动结束后随机调查了40名学生每人植树的棵数,根据调查获取的样本数据,制作了不完整的扇形统计图和条形统计图.请根据相关信息,解答下列问题:

(Ⅰ)扇形统计图中m的值是_____________,补全条形统计图
(Ⅱ)求抽取的这部分学生植树棵数的平均数;
(Ⅲ)若本次活动共有320名学生参加,估计植树棵数超过8棵的约有多少人。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】居民区内的“广场舞”引起媒体关注,小王想了解本小区居民对“广场舞”的看法,进行一次分四个层次的抽样调查(四个层次为:A,非常赞同;B.赞同但要有时间限制;C.无所谓;D.不赞同),并把调查结果绘制成如下两幅不完整的统计图,请根据统计图中的倍息解答下列问题:

(1)本次被抽查的居民人数是 人,将条形统计图补充完整.
(2)图中∠α的度数是 度;该小区有3000名居民,请估计对“广场舞”表示赞同(包括A层次和B层次)的大约有人
(3)据了解,甲、乙、丙、丁四位居民投不赞同票,小王想从这四位居民中随机选择两位了解具体情况,请用列表或画树状图的方法求出恰好选中甲和乙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春暖花开,树木萌芽,某种时令蔬菜的价格呈上升趋势,若这种蔬菜开始时的售价为每斤20元,并且每天涨价2元,从第六天开始,保持每斤30元的稳定价格销售,直到11天结束,该蔬菜退市.
(1)请写出该种蔬菜销售价格y与天数x之间的函数关系式;
(2)若该种蔬菜于进货当天售完,且这种蔬菜每斤进价z与天数x的关系为z=﹣![]() +12(1≤x≤11),且x为整数,那么该种蔬菜在第几天售出后,每斤获得利润最大?最大利润为多少?
+12(1≤x≤11),且x为整数,那么该种蔬菜在第几天售出后,每斤获得利润最大?最大利润为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
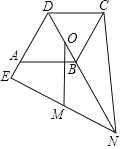
【题目】已知菱形 ABCD 中, ADC 120 , F 为 DB 延长线上一点, E 为 DA 延长线上一点, 且 BF DE , 连 CF 、 EF , 点 O 为 BD 的中点, 过 O 作 OM AB 交 EF 于 M , 若OM ![]() ,AE 1,则 AB 的长度为( )
,AE 1,则 AB 的长度为( )
A.![]() B.2C.
B.2C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
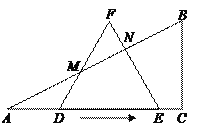
【题目】如图,已知Rt△ABC中,∠A=30°,AC=6.边长为4的等边△DEF沿射线AC运动(A、D、E、C四点共线).当等边△DEF的边DF、EF与Rt△ABC的边AB分别相交于点M、N(M、N不与A、B重合)时,
设AD=x.
(1)则△FMN的形状是 _______ ,△ADM的形状是 _______;
(2)△ABC与△DEF重叠部分的面积为y,求y关于x的函数解析式,并写出的取值范围;
(3)若以点M为圆心,MN为半径的圆与边AC、EF同时相切,求此时MN的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com