
【题目】已知关于x的一元二次方程ax2+bx+c=0的两实数根为x1,x2,根据一元二次方程解的意义和因式分解法解一元二次方程可知,x1,x2也是(x﹣x1)(x﹣x2)=0的两个实数根,所以ax2+bx+c=a(x﹣x1)(x﹣x2).
利用这个结论可以解决一些相关问题.
(1)实数范围内因式分解:
例:分解因式2x2+2x﹣1
解:令2x2+2x﹣1=0,解这个方程,得
![]() =
=![]() .
.
即x1=![]() ,x2=
,x2=![]() .
.
所以 2x2+2x﹣1=![]() .
.
试仿照上例在实数范围内分解因式:x2﹣6x+1;
(2)解不等式:x2+2x﹣1>0;
(3)灵活运用:
已知方程(x﹣a)(x﹣b)﹣x=0的两个实数根是c、d,求方程(2x﹣c)(2x﹣d)+2x=0的根.
【答案】(1)![]() ;(2)
;(2)![]() ,或
,或![]() ;(3)x1=
;(3)x1=![]() ,x2=
,x2=![]() .
.
【解析】
(1) 根据题意设x2-6x+1=0,解得x的值再代入方程即可.
(2) 根据题意设x2+2x-1=0,解得x的值再代入不等式,解得不等式组即可.
(3) 将方程(x﹣a)(x﹣b)﹣x=0的两根c、d代入方程,再把x=a代入方程即可解得方程的根.
解:(1)令x2-6x+1=0,解这个方程,得
![]() .
.
所以,x2-6x+1=![]() .
.
(2)令x2+2x-1=0,解这个方程,得
![]() .
.
所以 x2+2x-1=![]() .
.
所以 ![]() >0.
>0.
所以 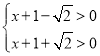 ,或
,或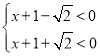 .
.
解这两个不等式组,得
![]() ,或
,或![]() .
.
(3)因为方程(x﹣a)(x﹣b)﹣x=0的两根是c、d,
所以 (x﹣a)(x﹣b)﹣x=(x-c)(x-d).
所以 (x-c)(x-d)+x=(x﹣a)(x﹣b).
因为当x=a时,代入上式,得
(a-c)(a-d)+a=(a﹣a)(a﹣b)=0,
所以x=a是方程(x-c)(x-d)+x=0的一个根,
同理,x=b也是方程(x-c)(x-d)+x=0的一个根.
所以方程 (x-c)(x-d)+x=0的两个根为x=a或b.
在方程(2x﹣c)(/span>2x﹣d)+2x=0中,设2x=y,得(y﹣c)(y﹣d)+y=0.
所以 y=a或b.
所以 2x=a或b,解得x1=![]() ,x2=
,x2=![]() .
.
所以,方程(2x﹣c)(2x﹣d)+2x=0的根是x1=![]() ,x2=
,x2=![]() .
.


 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案科目:初中数学 来源: 题型:
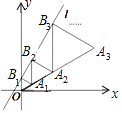
【题目】如图,在平面直角坐标系中,直线l:y=![]() 与y轴交于点B1,以OB1为一边在OB1右侧作等边三角形A1OB1,过点A1作A1B2平行于y轴,交直线l于点B2,以A1B2为一边在A1B2右侧作等边三角形A2A1B2,过点A2作A2B3平行于y轴,交直线l于点B3,以A2B3为一边在A2B3右侧作等边三角形A3A2B3,……则点A2019的纵坐标是( )
与y轴交于点B1,以OB1为一边在OB1右侧作等边三角形A1OB1,过点A1作A1B2平行于y轴,交直线l于点B2,以A1B2为一边在A1B2右侧作等边三角形A2A1B2,过点A2作A2B3平行于y轴,交直线l于点B3,以A2B3为一边在A2B3右侧作等边三角形A3A2B3,……则点A2019的纵坐标是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 与
与![]() 轴的一个交点为
轴的一个交点为![]() ,与
,与![]() 轴的交点
轴的交点![]() 在点
在点![]() 与点
与点![]() 之间(包含端点),顶点
之间(包含端点),顶点![]() 的坐标为
的坐标为![]() 。则下列结论:①
。则下列结论:①![]() ;②
;②![]() ;③对于任意实数
;③对于任意实数![]() ,
,![]() 总成立;④关于
总成立;④关于![]() 的方程
的方程![]() 没有实数根。其中结论正确的个数为()
没有实数根。其中结论正确的个数为()

A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
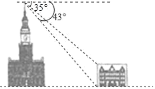
【题目】如图,甲、乙两座建筑物的水平距离BC为30m,从甲的顶部A处测得乙的顶部D处的俯角为35°测得底部C处的俯角为43°,求甲、乙两建筑物的高度AB和DC(结果取整数).
(参考数据:tan35°≈0.70,tan43°≈0.93)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为纪念建国70周年,某校举行班级歌咏比赛,歌曲有:《我爱你,中国》,《歌唱祖国》,《我和我的祖国》(分别用字母A,B,C依次表示这三首歌曲).比赛时,将A,B,C这三个字母分别写在3张无差别不透明的卡片正面上,洗匀后正面向下放在桌面上,八(1)班班长先从中随机抽取一张卡片,放回后洗匀,再由八(2)班班长从中随机抽取一张卡片,进行歌咏比赛.
(1)八(1)班抽中歌曲《我和我的祖国》的概率是__________;
(2)试用画树状图或列表的方法表示所有可能的结果,并求出八(1)班和八(2)班抽中不同歌曲的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线![]() 开口向下,与
开口向下,与![]() 轴交于点
轴交于点![]() ,顶点坐标为
,顶点坐标为![]() ,与
,与![]() 轴的交点在
轴的交点在![]() ,
,![]() 之间(包含端点),则下列结论:
之间(包含端点),则下列结论:
①![]() ;②
;②![]() ;③对于任意实数
;③对于任意实数![]() ,
,![]() 总成立;
总成立;
④关于![]() 的方程
的方程![]() 有两个不相等的实数根.
有两个不相等的实数根.
其中结论正确的个数是( )
A. 1个B. 2个
C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B是反比例函数y=![]() (x>0)图象上的两点,分别过A,B两点向x轴,y轴作垂线段,AD,BE两垂线段交于点G.若图中阴影部分的面积为3,则△OAB的面积为( )
(x>0)图象上的两点,分别过A,B两点向x轴,y轴作垂线段,AD,BE两垂线段交于点G.若图中阴影部分的面积为3,则△OAB的面积为( )
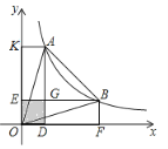
A.9B.10C.11D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组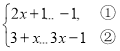
请结合题意填空,完成本题的解答。
(I)解不等式①,得________________
(Ⅱ)解不等式②,得:_____________________
(Ⅲ)把不等式①和②的解集在数轴上表示出来:

(IV)原不等式组的解集为___________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com