
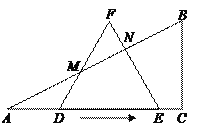
����Ŀ����ͼ����֪Rt��ABC�У���A��30�㣬AC��6���߳�Ϊ4�ĵȱߡ�DEF������AC�˶���A��D��E��C�ĵ㹲�ߣ�.���ȱߡ�DEF�ı�DF��EF��Rt��ABC�ı�AB�ֱ��ཻ�ڵ�M��N��M��N����A��B�غϣ�ʱ��
��AD=x��
��1�����FMN����״�� _______ ,��ADM����״�� _______��
��2����ABC���DEF�ص����ֵ����Ϊy����y����x�ĺ�������ʽ����д����ȡֵ��Χ��
��3�����Ե�MΪԲ�ģ�MNΪ�뾶��Բ���AC��EFͬʱ���У����ʱMN�ij���
���𰸡���1��ֱ�������� ��������������2��![]() ����3��
����3��![]()
��������
��1��ֱ�������Ρ�����������
��2���ߡ�AD���ǵ��������Σ�
��DM=AD=x �� FM=4-x.
�֡ߡ�FED=60�㣬��A=30�㣬 ���FNM=90��
��MN=MF��SinF=![]() ��FN=
��FN=![]() MF=
MF=![]() ��4-x��
��4-x��![]()
��0<x��2ʱ��![]()
��2��x<4ʱ�� CE=AE�DAC=4+x-6=x-2
�ߡ�BCE=90�㣬��PEA=60�㣬
��PC=![]()
��![]()
�� =S��DEF�DS��FMN�DS��PCE=![]()
��3������M��MG��AC�ڵ�G���ɣ�2����DM=x
�ߡ�MDG=60�㣬 ��MG=![]()
����MNF=90�㣬��MFN=60�㣬��MN=![]()
Ҫʹ�Ե�MΪԲ�ģ�MN��Ϊ�뾶��Բ���AC��EF���У�����MG=MN��
����![]() ���x=2��
���x=2��
Բ�İ뾶MN=![]()



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��A��B�Ƿ���������y��![]() ��x��0��ͼ���ϵ����㣬�ֱ��A��B������x�ᣬy�������߶Σ�AD��BE�����߶ν��ڵ�G����ͼ����Ӱ���ֵ����Ϊ3�����OAB�����Ϊ��������
��x��0��ͼ���ϵ����㣬�ֱ��A��B������x�ᣬy�������߶Σ�AD��BE�����߶ν��ڵ�G����ͼ����Ӱ���ֵ����Ϊ3�����OAB�����Ϊ��������
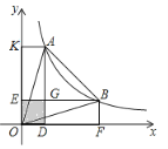
A.9B.10C.11D.12
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ⲻ��ʽ��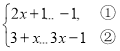
����������գ���ɱ���Ľ��
��I���ⲻ��ʽ�٣���________________
���ⲻ��ʽ�ڣ��ã�_____________________
���Ѳ���ʽ�ٺ͢ڵĽ⼯�������ϱ�ʾ������

��IV��ԭ����ʽ��Ľ⼯Ϊ___________________.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����в��ϣ��������
��2x��5��2+��3x+7��2=��5x+2��2
�⣺��m=2x��5��n=3x+7����m+n=5x+2
��ԭ���̿ɻ�Ϊm2+n2=��m+n��2
����mn=0������2x��5����3x+7��=0
��֮�ã�x1=![]() ��x2=��
��x2=��![]()
���������������ⷽ�̣�4x��5��2+��3x��2��2=��x��3��2
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
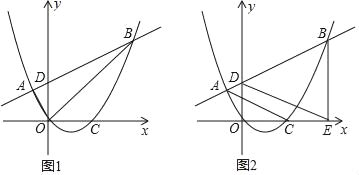
����Ŀ����ͼ��������y=ax2+bx������A����1��![]() ����ԭ�㣬��x������һ��C��2��0������D��0��m����y����������һ���㣬ֱ��AD������������һ��B��
����ԭ�㣬��x������һ��C��2��0������D��0��m����y����������һ���㣬ֱ��AD������������һ��B��
��1���������ߵĽ���ʽ��
��2����ͼ1������AO��BO������OAB�����Ϊ5����m��ֵ��
��3����ͼ2����BE��x����E������AC��DE����D���˶��仯ʱ��AC��DE��λ�ù�ϵ�Ƿ�仯����֤����Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ�����ͼ��A��2��0����C(0��12) ���㣬�ҶԳ���Ϊֱ��x=4. �趥��Ϊ��P����x�����һ����Ϊ��B.
��1������κ����Ľ���ʽ������P�����ꣻ
��2����ͼ����ֱ�� y=2x���Ƿ���ڵ�D��ʹ�ı���OPBDΪ�������Σ������ڣ������D�����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
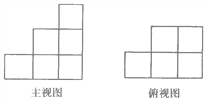
����Ŀ����һЩ��С��ͬ��С��������ɵļ����������ͼ����ͼ��ͼ29-29��ʾ.
(1)���㻭������������һ������ͼ.
(2)���������������С������Ŀ���Ϊn������д��n�����п���ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������Ϊ(![]() ����
����![]() )��������y��ax2��bx��c����M(2��0)��
)��������y��ax2��bx��c����M(2��0)��
(1)�����ߵı���ʽ��
(2)��A����������x��Ľ���(�����M�غ�)����B����������y��Ľ�������C��ֱ��y��x��1��һ��(����x���·�)����D�Ƿ���������y��![]() (k��0)ͼ����һ�������Ե�A��B��C��DΪ������ı�������������k��ֵ��
(k��0)ͼ����һ�������Ե�A��B��C��DΪ������ı�������������k��ֵ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����Rt��ABC��б��BCΪһ������ABC��ͬ����������BCEF���������ε�����ΪO������AO�����AB=4��AO=6![]() ����ôAC=_____��
����ôAC=_____��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com