
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕжаЃЌ![]() ЕФЖЅЕузјБъЗжБ№ЮЊ
ЕФЖЅЕузјБъЗжБ№ЮЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() .ЖЏЕу
.ЖЏЕу![]() ЃЌ
ЃЌ![]() ЭЌЪБДгЕу
ЭЌЪБДгЕу![]() ГіЗЂЃЌ
ГіЗЂЃЌ![]() би
би![]() ЃЌ
ЃЌ![]() биелЯп
биелЯп![]() ЃЌОљвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШвЦЖЏЃЌЕБвЛИіЖЏЕуЕНДяжеЕу
ЃЌОљвдУПУы1ИіЕЅЮЛГЄЖШЕФЫйЖШвЦЖЏЃЌЕБвЛИіЖЏЕуЕНДяжеЕу![]() ЪБЃЌСэвЛИіЖЏЕувВЫцжЎЭЃжЙвЦЖЏЃЌвЦЖЏЪБМфМЧЮЊ
ЪБЃЌСэвЛИіЖЏЕувВЫцжЎЭЃжЙвЦЖЏЃЌвЦЖЏЪБМфМЧЮЊ![]() УыЃЌСЌНг
УыЃЌСЌНг![]() .
.
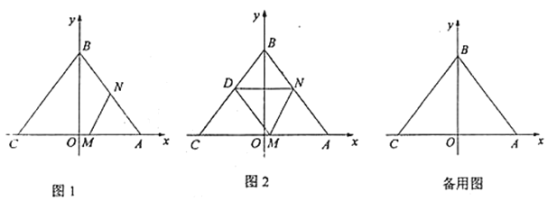
ЃЈЂёЃЉШчЭМ1ЃЌЕБЕу![]() вЦЖЏЕН
вЦЖЏЕН![]() жаЕуЪБЃЌЧѓДЫЪБ
жаЕуЪБЃЌЧѓДЫЪБ![]() ЕФжЕМА
ЕФжЕМА![]() ЕузјБъЃЛ
ЕузјБъЃЛ
ЃЈЂђЃЉдквЦЖЏЙ§ГЬжаЃЌНЋ![]() бижБЯп
бижБЯп![]() ЗелЃЌЕу
ЗелЃЌЕу![]() ЕФЖдГЦЕуЮЊ
ЕФЖдГЦЕуЮЊ![]() .
.
ЂйШчЭМ2ЃЌЕБЕу![]() ЧЁКУТфдк
ЧЁКУТфдк![]() БпЩЯЕФЕу
БпЩЯЕФЕу![]() ДІЪБЃЌЧѓДЫЪБ
ДІЪБЃЌЧѓДЫЪБ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЂкЕБЕу![]() вЦЖЏЕНЕу
вЦЖЏЕНЕу![]() ЪБЃЌЕу
ЪБЃЌЕу![]() ТфдкЕу
ТфдкЕу![]() ДІЃЌЧѓДЫЪБЕу
ДІЃЌЧѓДЫЪБЕу![]() ЕФзјБъЃЈжБНгаДГіНсЙћМДПЩЃЉ.
ЕФзјБъЃЈжБНгаДГіНсЙћМДПЩЃЉ.
ЁОД№АИЁПЃЈЂёЃЉ![]() ,Еу
,Еу![]() зјБъЮЊ
зјБъЮЊ![]() ; ЃЈЂђЃЉЂй
; ЃЈЂђЃЉЂй![]() ; Ђк
; Ђк![]() ЕузјБъЮЊ
ЕузјБъЮЊ![]()
ЁОНтЮіЁП
(1)ИљОнЕуЕФзјБъЃЌвдЧѓЕУABЕФГЄЃЌгЩгкNЪЧABЕФжаЕуЃЌПЩЕУANЕФГЄЖШЃЌДгЖјЧѓГіtЃЌМДПЩЧѓMЕуКњзјБъ;
(2)ЂйгЩЗзХЕФаджЪПЩЕУЫФБпаЮ![]() ЮЊСтаЮЃЌдђга
ЮЊСтаЮЃЌдђга![]() жсЃЌПЩЕУЕН
жсЃЌПЩЕУЕН![]() ЃЌМД
ЃЌМД![]() ЃЌДгЖјЧѓГіt.
ЃЌДгЖјЧѓГіt.
ЂкИљОнЯрЫЦПЩвдЧѓГіN(![]() )ЃЌЩшE(x,y),ИљОнЙДЙЩЖЈРэСаГіЗНГЬзщ:EM=6,EN=5,НтЕУМДПЩЧѓГіЕуE.
)ЃЌЩшE(x,y),ИљОнЙДЙЩЖЈРэСаГіЗНГЬзщ:EM=6,EN=5,НтЕУМДПЩЧѓГіЕуE.
ЃЈЂёЃЉЁп![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ![]() ЃЌЁр
ЃЌЁр![]() .
.
ЕБЕу![]() вЦЖЏЕН
вЦЖЏЕН![]() жаЕуЪБЃЌгЩЬтвтПЩЕУ
жаЕуЪБЃЌгЩЬтвтПЩЕУ![]() ЃЌ
ЃЌ
Ёр![]() .
.
Ёп![]() ЃЌ
ЃЌ
ЁрЕу![]() зјБъЮЊ
зјБъЮЊ![]() .
.
ЃЈЂђЃЉЂйгЩЬтвтПЩЕУ![]() ЃЌ
ЃЌ
Ёп![]() бижБЯп
бижБЯп![]() ЗелЃЌЕу
ЗелЃЌЕу![]() ТфдкЕу
ТфдкЕу![]() ДІЃЌ
ДІЃЌ
Ёр![]() ЃЌ
ЃЌ
ЁрЫФБпаЮ![]() ЮЊСтаЮЃЌ
ЮЊСтаЮЃЌ
Ёр![]() ЃЌ
ЃЌ![]() жсЃЌ
жсЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
НтЕУ![]() .
.
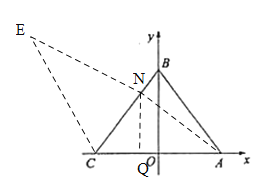
ЃЈЂђЃЉЂкЙ§NзіXжсЕФДЙЯпЃЌДЙзуЮЊQЃЌгЩЁїCNQЁзЁїBCOЃЌ
гжЁпBN=1,AC=6,BC=5,
Ёр![]() ,ЁрN(
,ЁрN(![]() )ЃЌ
)ЃЌ
ЩшE(x,y),ЧвCE=6,EN=5,
дђ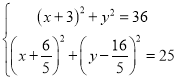
НтЕУЃК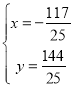
![]() ЕузјБъЮЊ
ЕузјБъЮЊ![]() .
.


 ЦЗбЇЫЋгХОэЯЕСаД№АИ
ЦЗбЇЫЋгХОэЯЕСаД№АИ аЁбЇЦкФЉГхДЬ100ЗжЯЕСаД№АИ
аЁбЇЦкФЉГхДЬ100ЗжЯЕСаД№АИ ЦкФЉИДЯАМьВтЯЕСаД№АИ
ЦкФЉИДЯАМьВтЯЕСаД№АИ ГЌФмбЇЕфЕЅдЊЦкжаЦкФЉзЈЬтГхДЬ100ЗжЯЕСаД№АИ
ГЌФмбЇЕфЕЅдЊЦкжаЦкФЉзЈЬтГхДЬ100ЗжЯЕСаД№АИ ЛЦИд360ЖШЖЈжЦУмОэЯЕСаД№АИ
ЛЦИд360ЖШЖЈжЦУмОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯA=90ЁуЃЌAB=2cmЃЌAC=4cmЃЎЖЏЕуPДгЕуAГіЗЂЃЌбиABЗНЯђвд1cm/sЕФЫйЖШЯђЕуBдЫЖЏЃЌЖЏЕуQДгЕуBЭЌЪБГіЗЂЃЌбиBAЗНЯђвд1cm/sЕФЫйЖШЯђЕуAдЫЖЏЃЎЕБЕуPЕНДяЕуBЪБЃЌPЃЌQСНЕуЭЌЪБЭЃжЙдЫЖЏЃЌвдAPЮЊвЛБпЯђЩЯзїе§ЗНаЮAPDEЃЌЙ§ЕуQзїQFЁЮBCЃЌНЛACгкЕуFЃЎЩшЕуPЕФдЫЖЏЪБМфЮЊtsЃЌе§ЗНаЮКЭЬнаЮжиКЯВПЗжЕФУцЛ§ЮЊScm2ЃЎ
ЃЈ1ЃЉЕБt=ЁЁ_________ЁЁsЪБЃЌЕуPгыЕуQжиКЯЃЛ
ЃЈ2ЃЉЕБt=ЁЁ_________ЁЁsЪБЃЌЕуDдкQFЩЯЃЛ
ЃЈ3ЃЉЕБЕуPдкQЃЌBСНЕужЎМфЃЈВЛАќРЈQЃЌBСНЕуЃЉЪБЃЌЧѓSгыtжЎМфЕФКЏЪ§ЙиЯЕЪНЃЎ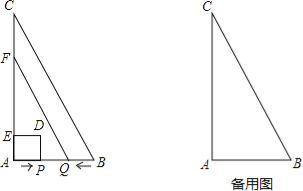
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
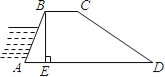
ЁОЬтФПЁПШчЭМЃЌФГКгЕЬЕФКсЖЯУцЪЧЬнаЮABCDЃЌBCЁЮADЃЌBEЁЭADгкЕуEЃЌAB=50УзЃЌBC=30УзЃЌЁЯA=60ЁуЃЌЁЯD=30ЁуЃЎЧѓADЕФГЄЖШЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊМЭФюНЈЙњ70жмФъЃЌФГаЃОйааАрМЖИшгНБШШќЃЌИшЧњгаЃКЁЖЮвАЎФуЃЌжаЙњЁЗЃЌЁЖИшГЊзцЙњЁЗЃЌЁЖЮвКЭЮвЕФзцЙњЁЗЃЈЗжБ№гУзжФИAЃЌBЃЌCвРДЮБэЪОетШ§ЪзИшЧњЃЉЃЎБШШќЪБЃЌНЋAЃЌBЃЌCетШ§ИізжФИЗжБ№аДдк3еХЮоВюБ№ВЛЭИУїЕФПЈЦЌе§УцЩЯЃЌЯДдШКѓе§УцЯђЯТЗХдкзРУцЩЯЃЌАЫЃЈ1ЃЉАрАрГЄЯШДгжаЫцЛњГщШЁвЛеХПЈЦЌЃЌЗХЛиКѓЯДдШЃЌдйгЩАЫЃЈ2ЃЉАрАрГЄДгжаЫцЛњГщШЁвЛеХПЈЦЌЃЌНјааИшгНБШШќЃЎ
ЃЈ1ЃЉАЫЃЈ1ЃЉАрГщжаИшЧњЁЖЮвКЭЮвЕФзцЙњЁЗЕФИХТЪЪЧ__________ЃЛ
ЃЈ2ЃЉЪдгУЛЪїзДЭМЛђСаБэЕФЗНЗЈБэЪОЫљгаПЩФмЕФНсЙћЃЌВЂЧѓГіАЫЃЈ1ЃЉАрКЭАЫЃЈ2ЃЉАрГщжаВЛЭЌИшЧњЕФИХТЪЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊХзЮяЯп![]() ПЊПкЯђЯТЃЌгы
ПЊПкЯђЯТЃЌгы![]() жсНЛгкЕу
жсНЛгкЕу![]() ЃЌЖЅЕузјБъЮЊ
ЃЌЖЅЕузјБъЮЊ![]() ЃЌгы
ЃЌгы![]() жсЕФНЛЕудк
жсЕФНЛЕудк![]() ЃЌ
ЃЌ![]() жЎМфЃЈАќКЌЖЫЕуЃЉЃЌдђЯТСаНсТлЃК
жЎМфЃЈАќКЌЖЫЕуЃЉЃЌдђЯТСаНсТлЃК
Ђй![]() ЃЛЂк
ЃЛЂк![]() ЃЛЂлЖдгкШЮвтЪЕЪ§
ЃЛЂлЖдгкШЮвтЪЕЪ§![]() ЃЌ
ЃЌ![]() змГЩСЂЃЛ
змГЩСЂЃЛ
ЂмЙигк![]() ЕФЗНГЬ
ЕФЗНГЬ![]() гаСНИіВЛЯрЕШЕФЪЕЪ§Иљ.
гаСНИіВЛЯрЕШЕФЪЕЪ§Иљ.
ЦфжаНсТле§ШЗЕФИіЪ§ЪЧЃЈ ЃЉ
A. 1ИіB. 2Иі
C. 3ИіD. 4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкУПИіаЁе§ЗНаЮЕФБпГЄЮЊ1ЕФЭјИёжаЃЌЕу![]() ЖМдкИёЕуЩЯЁЃ
ЖМдкИёЕуЩЯЁЃ

ЃЈЂёЃЉACЕФГЄЪЧ_____________ЃЛ
ЃЈЂђЃЉНЋЫФБпаЮ![]() елЕўЃЌЪЙЕуCгыЕу4жиКЯЃЌелКлEFНЛBCгкЕуEЃЌНЛADгкЕуFЃЌЕуDЕФЖдгІЕуЮЊQЃЌЕУЮхБпаЮ
елЕўЃЌЪЙЕуCгыЕу4жиКЯЃЌелКлEFНЛBCгкЕуEЃЌНЛADгкЕуFЃЌЕуDЕФЖдгІЕуЮЊQЃЌЕУЮхБпаЮ![]() .ЧыгУЮоПЬЖШЕФжБГпдкЭјИёжаЛГіелЕўКѓЕФЮхБпаЮЃЌВЂМђвЊЫЕУїЕу
.ЧыгУЮоПЬЖШЕФжБГпдкЭјИёжаЛГіелЕўКѓЕФЮхБпаЮЃЌВЂМђвЊЫЕУїЕу![]() ЕФЮЛжУЪЧШчКЮевЕНЕФ____________________.
ЕФЮЛжУЪЧШчКЮевЕНЕФ____________________.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌAЃЌBЪЧЗДБШР§КЏЪ§yЃН![]() ЃЈxЃО0ЃЉЭМЯѓЩЯЕФСНЕуЃЌЗжБ№Й§AЃЌBСНЕуЯђxжсЃЌyжсзїДЙЯпЖЮЃЌADЃЌBEСНДЙЯпЖЮНЛгкЕуGЃЎШєЭМжавѕгАВПЗжЕФУцЛ§ЮЊ3ЃЌдђЁїOABЕФУцЛ§ЮЊЃЈЁЁЁЁЃЉ
ЃЈxЃО0ЃЉЭМЯѓЩЯЕФСНЕуЃЌЗжБ№Й§AЃЌBСНЕуЯђxжсЃЌyжсзїДЙЯпЖЮЃЌADЃЌBEСНДЙЯпЖЮНЛгкЕуGЃЎШєЭМжавѕгАВПЗжЕФУцЛ§ЮЊ3ЃЌдђЁїOABЕФУцЛ§ЮЊЃЈЁЁЁЁЃЉ
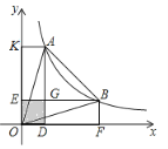
A.9B.10C.11D.12
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌжБЯпyЃНx+mгыЫЋЧњЯпyЃН![]() ЯрНЛгкAЃЈ2ЃЌ1ЃЉЃЌBСНЕуЃЎ
ЯрНЛгкAЃЈ2ЃЌ1ЃЉЃЌBСНЕуЃЎ
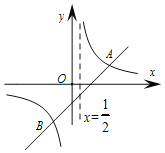
ЃЈ1ЃЉЧѓГівЛДЮКЏЪ§гыЗДБШР§КЏЪ§ЕФНтЮіЪНЃЌВЂЧѓГіBЕузјБъЃЛ
ЃЈ2ЃЉШєPЮЊжБЯпxЃН![]() ЩЯвЛЕуЃЌЕБЁїAPBЕФУцЛ§ЮЊ6ЪБЃЌЧыЧѓГіЕуPЕФзјБъЃЎ
ЩЯвЛЕуЃЌЕБЁїAPBЕФУцЛ§ЮЊ6ЪБЃЌЧыЧѓГіЕуPЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСЯТСаВФСЯЃЌНтД№ЮЪЬт
ЃЈ2xЉ5ЃЉ2+ЃЈ3x+7ЃЉ2=ЃЈ5x+2ЃЉ2
НтЃКЩшm=2xЉ5ЃЌn=3x+7ЃЌдђm+n=5x+2
дђдЗНГЬПЩЛЏЮЊm2+n2=ЃЈm+nЃЉ2
Ыљвдmn=0ЃЌМДЃЈ2xЉ5ЃЉЃЈ3x+7ЃЉ=0
НтжЎЕУЃЌx1=![]() ЃЌx2=Љ
ЃЌx2=Љ![]()
ЧыРћгУЩЯЪіЗНЗЈНтЗНГЬЃЈ4xЉ5ЃЉ2+ЃЈ3xЉ2ЃЉ2=ЃЈxЉ3ЃЉ2
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com