
【题目】已知菱形 ABCD 中, ADC 120 , F 为 DB 延长线上一点, E 为 DA 延长线上一点, 且 BF DE , 连 CF 、 EF , 点 O 为 BD 的中点, 过 O 作 OM AB 交 EF 于 M , 若OM ![]() ,AE 1,则 AB 的长度为( )
,AE 1,则 AB 的长度为( )
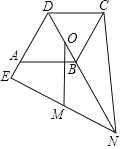
A.![]() B.2C.
B.2C.![]() D.
D.![]()
【答案】C
【解析】
连接CM,CO,CE,判定△EDC≌△NBC,即可得到∠DCE=∠BCN,EC=NC,进而得出△ECN为等边三角形,依据∠CMO=∠CED,∠CDE=∠COM=120°,可得△CDE∽△COM,再根据相似三角形的性质,即可得到AD,AB的长.
解:如图,连接CM,CO,CE,
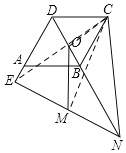
∵菱形ABCD中,∠ADC=120°,N为DB延长线上一点,
∴∠ADC=∠NBC=120°,CD=CB,而DE=BN,
∴△EDC≌△NBC(SAS),
∴∠DCE=∠BCN,EC=NC,
又∵∠DCE+∠ECB=60°,
∴∠BCN+∠ECB=60°,
∴∠ECN=60°,
∴△ECN为等边三角形,
∴∠CNM=60°,
∴∠CNM+∠COM=180°,
∴M,N,O,C四点共圆,
∴∠CNB=∠CMO,
又∵∠CNB=∠CED,
∴∠CMO=∠CED,
又∵∠CDE=∠COM=120°,
∴△CDE∽△COM,
![]() ,即
,即![]()
解得![]()
又∵AE=1,
![]()
故选:C


 全优点练单元计划系列答案
全优点练单元计划系列答案科目:初中数学 来源: 题型:
【题目】如图,A,B是反比例函数y=![]() (x>0)图象上的两点,分别过A,B两点向x轴,y轴作垂线段,AD,BE两垂线段交于点G.若图中阴影部分的面积为3,则△OAB的面积为( )
(x>0)图象上的两点,分别过A,B两点向x轴,y轴作垂线段,AD,BE两垂线段交于点G.若图中阴影部分的面积为3,则△OAB的面积为( )
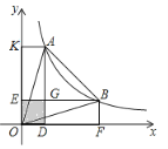
A.9B.10C.11D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=x+m与双曲线y=![]() 相交于A(2,1),B两点.
相交于A(2,1),B两点.
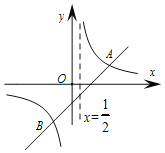
(1)求出一次函数与反比例函数的解析式,并求出B点坐标;
(2)若P为直线x=![]() 上一点,当△APB的面积为6时,请求出点P的坐标.
上一点,当△APB的面积为6时,请求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
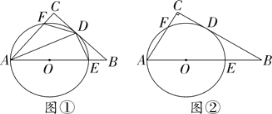
【题目】在△ABC中,∠C=90°,以AB上一点O为圆心,OA为半径的圆与BC相切于点D,分别交AB,AC于点E,F.
(1)如图①,连接AD,若∠CAD=25°,求∠B的大小;
(2)如图②,若点F为弧AD的中点,⊙O的半径为2,求AB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
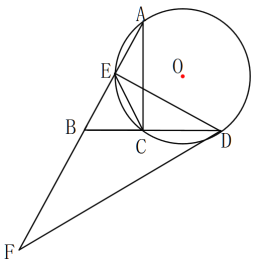
【题目】如图,在 RtABC 中,ACB 90 ,点 E 为 AB 中点,经过 A 、C 、E 三点的⊙O 与 BC的延长线相交于点 D ,过点 D 的直线交 AB 的延长线于点 F ,且FDB CED 。
(1)求证: DF 为⊙O 的切线;
(2)若 AE ![]() ,CD 1,求 DF ;
,CD 1,求 DF ;
(3)若 BF mBE ,求sin BAC (用含 m 的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组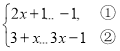
请结合题意填空,完成本题的解答。
(I)解不等式①,得________________
(Ⅱ)解不等式②,得:_____________________
(Ⅲ)把不等式①和②的解集在数轴上表示出来:

(IV)原不等式组的解集为___________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,解答问题
(2x﹣5)2+(3x+7)2=(5x+2)2
解:设m=2x﹣5,n=3x+7,则m+n=5x+2
则原方程可化为m2+n2=(m+n)2
所以mn=0,即(2x﹣5)(3x+7)=0
解之得,x1=![]() ,x2=﹣
,x2=﹣![]()
请利用上述方法解方程(4x﹣5)2+(3x﹣2)2=(x﹣3)2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,顶点为(![]() ,-
,-![]() )的抛物线y=ax2+bx+c过点M(2,0).
)的抛物线y=ax2+bx+c过点M(2,0).
(1)求抛线的表达式;
(2)点A是抛物线与x轴的交点(不与点M重合),点B是抛物线与y轴的交点,点C是直线y=x+1上一点(处于x轴下方),点D是反比例函数y=![]() (k>0)图象上一点,若以点A,B,C,D为顶点的四边形是菱形,求k的值.
(k>0)图象上一点,若以点A,B,C,D为顶点的四边形是菱形,求k的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com