
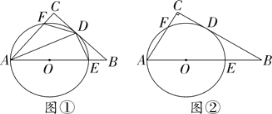
【题目】在△ABC中,∠C=90°,以AB上一点O为圆心,OA为半径的圆与BC相切于点D,分别交AB,AC于点E,F.
(1)如图①,连接AD,若∠CAD=25°,求∠B的大小;
(2)如图②,若点F为弧AD的中点,⊙O的半径为2,求AB的长.
【答案】(1)∠B=40°;(2)AB= 6.
【解析】
(1)连接OD,由在△ABC中, ∠C=90°,BC是切线,易得AC∥OD,即可求得∠CAD=∠ADO,继而求得答案;
(2)首先连接OF,OD,由AC∥OD得∠OFA=∠FOD,由点F为弧AD的中点,易得△AOF是等边三角形,继而求得答案.
解:(1)如解图①,连接OD,
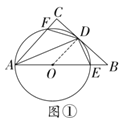
∵BC切⊙O于点D,
∴∠ODB=90°,
∵∠C=90°,
∴AC∥OD,
∴∠CAD=∠ADO,
∵OA=OD,
∴∠DAO=∠ADO=∠CAD=25°,
∴∠DOB=∠CAO=∠CAD+∠DAO=50°,
∵∠ODB=90°,
∴∠B=90°-∠DOB=90°-50°=40°;
(2)如解图②,连接OF,OD,
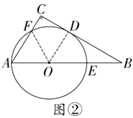
∵AC∥OD,
∴∠OFA=∠FOD,
∵点F为弧AD的中点,
∴∠AOF=∠FOD,
∴∠OFA=∠AOF,
∴AF=OA,
∵OA=OF,
∴△AOF为等边三角形,
∴∠FAO=60°,则∠DOB=60°,
∴∠B=30°,
∵在Rt△ODB中,OD=2,
∴OB=4,
∴AB=AO+OB=2+4=6.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:初中数学 来源: 题型:
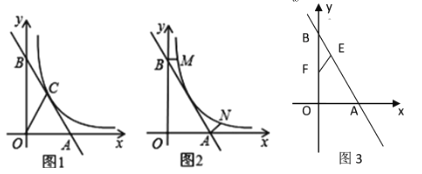
【题目】如图1,一次函数y=2x+4的图象交x轴于点A,交y轴于点B,与反比例函数y=![]() (x>0)的图象交于点C,连OC,若S△AOC=2.
(x>0)的图象交于点C,连OC,若S△AOC=2.
(1)求反比例函数的解析式;
(2)如图3,点E, F分别是线段AB和线段OB上的动点,点E从点B出发,沿线段BA运动,点F从点O出发,沿线段OB运动,速度都是每秒1个单位长度。运动时间为t秒,当其中一点到达终点后,另一点也随之停止运动.是否存在某个时刻。使得△BEF是直角三角形?若存在,求出t的值若不存在,请说明理由:
(3)如图2,过点B作BM⊥OB交反比例函数y=![]() (x>0)的图象于点M,点N为反比例函数 y=
(x>0)的图象于点M,点N为反比例函数 y=![]() (x>0)的图象上一点,∠ABM =∠BAN,求直线AN的解析式,
(x>0)的图象上一点,∠ABM =∠BAN,求直线AN的解析式,
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将下列各式因式分解
(1)2a3b﹣8ab3
(2)﹣x3+x2y﹣![]() xy2
xy2
(3)(7x2+2y2)2﹣(2x2+7y2)2
(4)(x2+4x)2+(x2+4x)﹣6
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知点D与点A(0,6)、B(0,﹣4)、C(x,y)是平行四边形的四个顶点,其中x、y满3x﹣4y+12=0,则CD的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
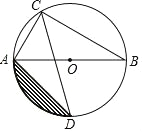
【题目】如图所示,AB是⊙O的直径,∠B=30°,弦BC=6,∠ACB的平分线交⊙O于D,连AD.
(1)求直径AB的长.
(2)求阴影部分的面积(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线l:y=kx和抛物线C:y=ax2+bx+1.
(1)当k=1,b=1时,抛物线C:y=ax2+bx+1的顶点在直线l:y=kx上,求a的值;
(2)若把直线l向上平移k2+1个单位长度得到直线r,则无论非零实数k取何值,直线r与抛物线C都只有一个交点;
(i)求此抛物线的解析式;
(ii)若P是此抛物线上任一点,过点P作PQ∥y轴且与直线y=2交于点Q,O为原点,
求证:OP=PQ.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c交x轴于A、B 两点,交 y 轴于 C点,其中﹣2<h<﹣1,﹣1<xB<0,下列结论:①abc>0;②4a﹣2b+c>0;③5a+2c>3b;④(4a﹣b)(2a+b)<0;正确的有( )个.
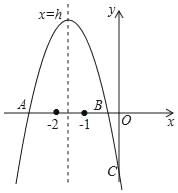
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,D是边AB上一点,且∠A=2∠DCB.E是BC边上的一点,以EC为直径的⊙O经过点D.
(1)求证:AB是⊙O的切线;
(2)若CD的弦心距为1,BE=EO,求BD的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com