
【题目】如图所示,AB是⊙O的直径,∠B=30°,弦BC=6,∠ACB的平分线交⊙O于D,连AD.
(1)求直径AB的长.
(2)求阴影部分的面积(结果保留π).
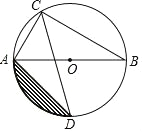
【答案】(1)4;(2)3π﹣6;
【解析】
(1)根据直径所对的圆周角是直角推知∠ACB=90°,然后在直角三角形ABC中利用边角关系、勾股定理来求直径AB的长度;
(2)连接OD.利用(1)中求得AB=4![]() 可以推知OA=OD=2
可以推知OA=OD=2![]() ;然后由角平分线的性质求得∠AOD=90°;最后由扇形的面积公式、三角形的面积公式可以求得阴影部分的面积=S扇形△AOD-S△AOD.
;然后由角平分线的性质求得∠AOD=90°;最后由扇形的面积公式、三角形的面积公式可以求得阴影部分的面积=S扇形△AOD-S△AOD.
(1)∵AB为⊙O的直径,
∴∠ACB=90°,
∵∠B=30°,
∴AB=2AC,
∵AB2=AC2+BC2,
∴AB2=![]() AB2+62,
AB2+62,
∴AB=4![]() .
.
(2)连接OD.
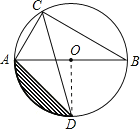
∵AB=4![]() ,
,
∴OA=OD=2![]() ,
,
∵CD平分∠ACB,∠ACB=90°,
∴∠ACD=45°,
∴∠AOD=2∠ACD=90°,
∴S△AOD=![]() OAOD=
OAOD=![]() ×2
×2![]() ×2
×2![]() =6,
=6,
∴S扇形△AOD=![]() πOD2=
πOD2=![]() π(2
π(2![]() )2=3π,
)2=3π,
∴阴影部分的面积=S扇形△AOD-S△AOD=3π-6.


 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案科目:初中数学 来源: 题型:
【题目】如图,转盘被等分成六个扇形区域,并在上面依次写上数字:![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() .转盘指针的位置固定,转动转盘后任其自由停止.
.转盘指针的位置固定,转动转盘后任其自由停止.
![]() 当停止转动时,指针指向奇数区域的概率是多少?
当停止转动时,指针指向奇数区域的概率是多少?
![]() 请你用这个转盘设计一个游戏(六等分扇形不变),使自由转动的转盘停止时,指针指向的区域的概率为
请你用这个转盘设计一个游戏(六等分扇形不变),使自由转动的转盘停止时,指针指向的区域的概率为![]() ,并说明你的设计理由.(设计方案可用图示表示,也可以用文字表述)
,并说明你的设计理由.(设计方案可用图示表示,也可以用文字表述)

查看答案和解析>>
科目:初中数学 来源: 题型:
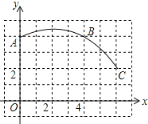
【题目】甲、乙两车从A地出发,匀速驶向B地.甲车以80km/h的速度行驶1h后,乙车才沿相同路线行驶.乙车先到达B地并停留1h后,再以原速按原路返回,直至与甲车相遇.在此过程中,两车之间的距离y(km)与乙车行驶时间x(h)之间的函数关系如图所示.下列说法:①乙车的速度是120km/h;②m=160;③点H的坐标是(7,80);④n=7.5.
其中说法正确的是( )

A. ①②③ B. ①②④ C. ①③④ D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A(4,3)是反比例函数y=![]() 在第一象限图象上一点,连接OA,过A作AB∥x轴,截取AB=OA(B在A右侧),连接OB,交反比例函数y=
在第一象限图象上一点,连接OA,过A作AB∥x轴,截取AB=OA(B在A右侧),连接OB,交反比例函数y=![]() 的图象于点P.
的图象于点P.
(1)求反比例函数y=![]() 的表达式;
的表达式;
(2)求点B的坐标;
(3)求△OAP的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,平面直角坐标系中,点A(2,9),B(2,3),C(3,2),D(9,2)在⊙P上,Q是⊙P上的一个动点.
(1)在图中标出圆心P位置,写出点P坐标;
(2)Q点在圆上坐标为何值时,△ABQ是直角三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一段圆弧与长度为1的正方形网格的交点是A、B、C.
(1)请完成以下操作:
①以点O为原点,垂直和水平方向为轴,网格边长为单位长,建立平面直角坐标系;
②根据图形提供的信息,标出该圆弧所在圆的圆心D,并连接AD、CD;
(2)请在(1)的基础上,完成下列填空:⊙D的半径为__________;点(6,–2)在⊙D__________;(填“上”、“内”、“外”)∠ADC的度数为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
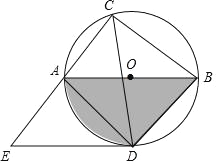
【题目】如图,⊙O的直径AB=12,弦AC=6,∠ACB的平分线交⊙O于D,过点D作DE∥AB交CA的延长线于点E,连接AD,BD.
(1)由AB,BD,![]() 围成的阴影部分的面积是 ;
围成的阴影部分的面积是 ;
(2)求线段DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明同学在学习了全等三角形的相关知识后发现,只用两把完全相同的长方形直尺就可以作出一个角的平分线.如图:一把直尺压住射线OB,另一把直尺压住射线OA并且与第一把直尺交于点P,小明说:“射线OP就是∠BOA的角平分线.”他这样做的依据是( )

A. 角的内部到角的两边的距离相等的点在角的平分线上
B. 角平分线上的点到这个角两边的距离相等
C. 三角形三条角平分线的交点到三条边的距离相等
D. 以上均不正确
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com