
【题目】如图,⊙O的直径AB=12,弦AC=6,∠ACB的平分线交⊙O于D,过点D作DE∥AB交CA的延长线于点E,连接AD,BD.
(1)由AB,BD,![]() 围成的阴影部分的面积是 ;
围成的阴影部分的面积是 ;
(2)求线段DE的长.
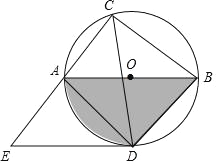
【答案】(1)9π+18;(2)DE=![]() +6;
+6;
【解析】
(1)根据题意作出合适的辅助线,然后根据题目中的数据和图形,即可求得阴影部分的面积;
(2)根据题意和图形,利用平行线的性质和特殊角的三角函数可以求得DE的长.
(1)如图,连接OD,
∵⊙O的直径AB=12,弦AC=6,∠ACB的平分线交⊙O于D,
∴∠ADB=90°,AD=BD,
∴∠OBD=∠ODB=45°,
∴OB=OD=6,
∴由AB,BD,![]() 围成的阴影部分的面积是:
围成的阴影部分的面积是:![]() (
(![]()
![]() )=9π+18,
)=9π+18,
故答案为:9π+18;
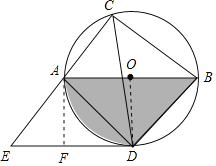
(2)如图,作AF⊥DE于点F,则AF=OD=6,
∵AB∥DE,∠OAD=45°,
∴∠ADF=∠OAD=45°,
∴DF=AF=6,
∵∠ACB=90°,AC=6,AB=12,
∴∠CBA=30°,
∴∠CAB=60°,
∵AB∥DE,
∴∠E=∠CAB=60°,
∵AF=6,∠AFE=90°,
∴EF=![]() =
=![]() =2
=2![]() ,
,
∴DE=EF+DF=2![]() +6.
+6.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,△ADB、△BCD都是等边三角形,点E,F分别是AB,AD上两个动点,满足AE=DF.连接BF与DE相交于点G,CH⊥BF,垂足为H,连接CG.若DG=![]() ,BG=
,BG=![]() ,且
,且![]() 、
、![]() 满足下列关系:
满足下列关系:![]() ,
,![]() ,则GH= .
,则GH= .

查看答案和解析>>
科目:初中数学 来源: 题型:
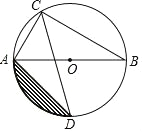
【题目】如图所示,AB是⊙O的直径,∠B=30°,弦BC=6,∠ACB的平分线交⊙O于D,连AD.
(1)求直径AB的长.
(2)求阴影部分的面积(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
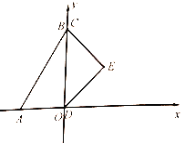
【题目】在平面直角坐标系中,一副含![]() 和
和![]() 角的三角板
角的三角板![]() 和
和![]() 如图摆放,边
如图摆放,边![]() 与
与![]() 重合,
重合,![]() .当点
.当点![]() 从点
从点![]() 出发沿
出发沿![]() 方向滑动时,点
方向滑动时,点![]() 同时从点
同时从点![]() 出发沿
出发沿![]() 轴正方向滑动.
轴正方向滑动.
![]() 设点
设点![]() 关于
关于![]() 的函数表达式为________.
的函数表达式为________.
![]() 连接
连接![]() .当点
.当点![]() 从点
从点![]() 滑动到点
滑动到点![]() 时,
时,![]() 的面积最大值为_______.
的面积最大值为_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,过点![]() 的直线
的直线![]() 与直线
与直线![]() 相交于点
相交于点![]() .
.
(1)直线![]() 的关系式为 ;直线
的关系式为 ;直线![]() 的关系式为 (直接写出答案,不必写过程).
的关系式为 (直接写出答案,不必写过程).
(2)求![]() 的面积.
的面积.
(3)若有一动点![]() 沿路线
沿路线![]() 运动,当
运动,当![]() 时,求点
时,求点![]() 坐标.
坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学有一块四边形的空地ABCD,如图所示,为了绿化环境,学校计划在空地上种植草皮,经测量∠A=90°,AB=3m,DA=4m,BC=12m,CD=13m.
(1)求出空地ABCD的面积.
(2)若每种植1平方米草皮需要200元,问总共需投入多少元?

查看答案和解析>>
科目:初中数学 来源: 题型:
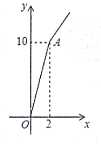
【题目】某玉米种子的价格为![]() 元/千克,如果一次购买2千克以上的种子,超过2千克部分的种子价格打8折,某科技人员对付款金额和购买量这两个变量的对应关系用列表法做了分析,并绘制出了函数图象,以下是该科技人员绘制的图象和表格的不完整资料,已知点A的坐标为
元/千克,如果一次购买2千克以上的种子,超过2千克部分的种子价格打8折,某科技人员对付款金额和购买量这两个变量的对应关系用列表法做了分析,并绘制出了函数图象,以下是该科技人员绘制的图象和表格的不完整资料,已知点A的坐标为![]() ,请你结合表格和图象:
,请你结合表格和图象:
付款金额 |
| 7.5 | 10 | 12 |
|
购买量 | 1 | 1.5 | 2 | 2.5 | 3 |
(1)![]() ,
,![]() ;
;
(2)求出当![]() 时,
时,![]() 关于
关于![]() 的函数解析式;
的函数解析式;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com