【题目】如图，
为等边三角形，点
，
分别在
，
上，
，
，
相交于点
，
于点
，
，
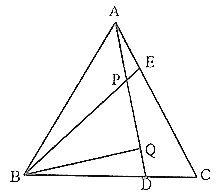
（1）求
的度数？
（2）求的长.
【答案】(1)60°;(2)14.
【解析】
(1)由题意证明△ABE≌△CAD,表示出∠AEB,再用内角和算出∠APE即为∠BPD的度数.
(2)根据(1)中条件得出∠QBP=30°,利用30°所对直角边是斜边一半算出BP,进而算出BE即为AD的长.
(1)∵△ABC是等边三角形,
∴∠BAE=∠C=60°,AB=AC,
又∵AE=CD,
∴△ABE≌△CAD(SAS)
∴∠CAD=∠ABE,
∵∠AEB=180°-∠ABE-60°,
∴∠APE=180°-(∠CAD+∠AEB)=180°-(∠CAD+180°-∠ABE-60°)=60°.
∴∠BPD=∠APE=60°.
(2)∵BQ⊥AD,∠BPD=60°,
∴∠PBQ=30°,
∵PQ=6,
∴BP=12,
∴BE=BP+PE=12+2=14.
∴AD=BE=14.
全能测控一本好卷系列答案科目：初中数学 来源： 题型：
【题目】如图(1)是一个长为2m，宽为2n的长方形，沿图中虚线剪成四个均匀的小长方形，然后按图(2)形状拼成一个正方形.
(1)你认为图(2)中的阴影部分的正方形的边长等于多少？
(2)观察图(2)，你能写出下列三个代数式之间的等量关系吗？代数式：
，
，
；
(3)已知：
，
，求的值.
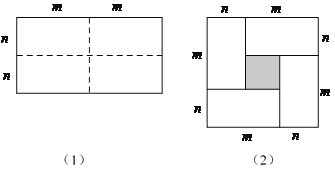
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，△ADB、△BCD都是等边三角形，点E，F分别是AB，AD上两个动点，满足AE=DF．连接BF与DE相交于点G，CH⊥BF，垂足为H，连接CG．若DG=
，BG=
，且
、
满足下列关系：
，
，则GH= ．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知点O到△ABC的两边AB，AC所在直线的距离相等，且OB＝OC.
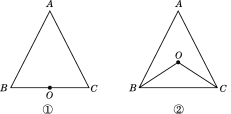
(1)如图①，若点O在BC上，求证：△ABC是等腰三角形．
(2)如图②，若点O在△ABC内部，求证AB＝AC.
(3)若点O在△ABC的外部，AB＝AC还成立吗？请画图说明．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，MN是⊙O的直径，∠AMN=40°，点B为弧AN的中点，点P是直径MN上的一个动点，如果PA+PB的最小值为
，那么⊙O的直径等于（ ）
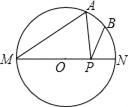
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知⊙O的直径为10，点A、点B、点C在⊙O上，∠CAB的平分线交⊙O于点D．
（1）如图①，若BC为⊙O的直径，AB=6，求AC，BD的长；
（2）如图②，若∠CAB=60°，CF⊥BD，①求证：CF是⊙O的切线；②求由弦CD、CB以及弧DB围成图形的面积．
查看答案和解析>>
科目：初中数学 来源： 题型：
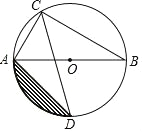
【题目】如图所示，AB是⊙O的直径，∠B=30°，弦BC=6，∠ACB的平分线交⊙O于D，连AD．
（1）求直径AB的长．
（2）求阴影部分的面积（结果保留π）．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
