[题目]如图.MN是⊙O的直径.∠AMN=40°.点B为弧AN的中点.点P是直径MN上的一个动点.如果PA+PB的最小值为.那么⊙O的直径等于( )A. 2 B. 3 C. 4 D. 5 题目和参考答案——青夏教育精英家教网—

【题目】如图，MN是⊙O的直径，∠AMN=40°，点B为弧AN的中点，点P是直径MN上的一个动点，如果PA+PB的最小值为，那么⊙O的直径等于（　　）

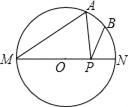
A. 2 B. 3 C. 4 D. 5

【答案】A

【解析】

首先利用在直线L上的同侧有两个点A、B，在直线L上有到A、B的距离之和最短的点存在，可以通过轴对称来确定，即作出其中一点关于直线L的对称点，对称点与另一点的连线与直线L的交点就是所要找的点P的位置，然后根据弧的度数发现一个等腰直角三角形计算．

解：作点B关于MN的对称点C，连接AC交MN于点P，则P点就是所求作的点．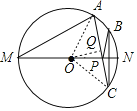

此时PA+PB最小，且等于AC的长．
连接OA，OC，
∵∠AMN=40°，
∴∠AON=80°，

的度数是80°，
则的度数是40°，
根据垂径定理得的度数是40°，
则∠AOC=120°，
作OQ⊥AC于点Q，

则∠AOQ=60°，AQ=AC= ,

∴OA=1,

∴MN=2OA=2，
故选：A．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】某水果生产基地销售苹果，提供两种购买方式供客户选择

方式：若客户缴纳元会费加盟为生产基地合作单位，则苹果成交价为元千克.

方式：若客户购买数量达到或超过千克，则成交价为元千克；若客户购买数量不足千克，则成交价为元千克.设客户购买苹果数量为（千克），所需费用为（元）.

（1）若客户按方式购买，请写出（元）与（千克）之间的函数表达式;（备注：按方式购买苹果所需费用生产基地合作单位会费苹果成交总价）

（2）如果购买数量超过千克，请说明客户选择哪种购买方式更省钱;

（3）若客户甲采用方式购买，客户乙采用方式购买，甲、乙共购买苹果千克，总费用共计元，则客户甲购买了多少千克苹果？

查看答案和解析>>

科目：初中数学 来源： 题型：

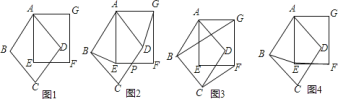
【题目】我们给定两个全等的正方形、，它们共顶点（如图），可以绕顶点旋转，，相交于点，以下各问题都以此为前提．

问题要求：

连接、（如图），求证：，；

连接、（如图），有三个结论：

①；

②；

③与位似．

请你从①，②，③三个结论中选择一个进行证明：

（说明：选①做对的得分，选②做对的得分，选③做对的得分）

连接、（如图），求的值．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，矩形中，点是线段上一动点，为的中点，的延长线交于．

求证：；

若厘米，厘米，当为何值时，四边形是菱形，并加以说明．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】如图，为等边三角形，点，分别在，上，，，相交于点，于点，，

（1）求的度数？

（2）求的长.

查看答案和解析>>

科目：初中数学 来源： 题型：

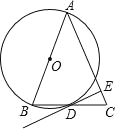
【题目】如图，在⊙O中，点P为直径BA延长线上一点，PD切⊙O于点D、过点B作BH⊥PH，点H为垂足，BH交⊙O于点C，连接BD，CD．

（1）求证：BD平分∠ABH；

（2）若CD=2，∠ABD=30°，求⊙O的直径的长．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】甲、乙两车从A地出发，匀速驶向B地．甲车以80km/h的速度行驶1h后，乙车才沿相同路线行驶．乙车先到达B地并停留1h后，再以原速按原路返回，直至与甲车相遇．在此过程中，两车之间的距离y（km）与乙车行驶时间x（h）之间的函数关系如图所示．下列说法：①乙车的速度是120km/h；②m=160；③点H的坐标是（7，80）；④n=7.5．

其中说法正确的是（　　）