
【题目】我们给定两个全等的正方形![]() 、
、![]() ,它们共顶点
,它们共顶点![]() (如图
(如图![]() ),可以绕顶点
),可以绕顶点![]() 旋转,
旋转,![]() ,
,![]() 相交于点
相交于点![]() ,以下各问题都以此为前提.
,以下各问题都以此为前提.
问题要求:
![]() 连接
连接![]() 、
、![]() (如图
(如图![]() ),求证:
),求证:![]() ,
,![]() ;
;
![]() 连接
连接![]() 、
、![]() (如图
(如图![]() ),有三个结论:
),有三个结论:
①![]() ;
;
②![]() ;
;
③![]() 与
与![]() 位似.
位似.
请你从①,②,③三个结论中选择一个进行证明:
(说明:选①做对的得![]() 分,选②做对的得
分,选②做对的得![]() 分,选③做对的得
分,选③做对的得![]() 分)
分)
![]() 连接
连接![]() 、
、![]() (如图
(如图![]() ),求
),求![]() 的值.
的值.
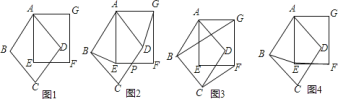
【答案】(1)证明见解析;(2)①证明见解析;②证明见解析;③![]() .
.
【解析】
(1)根据正方形的性质,即可得AB=AD,∠BAE=90°﹣∠EAD=∠DAG,AE=AG,由边角边判定方法即可证得△ABE≌△ADG,即BE=DG;∵△ABE≌△ADG,AB⊥AD,AE⊥AG,所以△ADG可以看成由△ABE绕顶点A旋转90°,即BE⊥DG;
(2)根据等边对等角即可证得BG∥CF;根据平行线的性质可的对应角相等,即可证得②△ABG∽△PCF;续②连接AP交GF的延长线于Q1,交BC的延长线于Q2,由位似的性质即可求得;
(3)连接AC,AF,CF.可证得△ABE∽△ACF,根据相似三角形的性质即可求得.
(1)∵AB=AD,∠BAE=90°﹣∠EAD=∠DAG,AE=AG,∴△ABE≌△ADG,即BE=DG.
分别延长GD,BE交于点M交EF于点N.
∵∠MEN+∠ENM=∠MEN+∠AGD=∠BEA+∠NEM=90°,∴BE⊥GD.
(∵△ABE≌△ADG,AB⊥AD,AE⊥AG,∴△ADG可以看成由△ABE绕顶点A旋转90°,即BE⊥DG.)
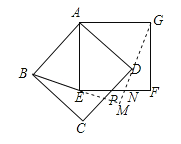
(2)①∵AB=AG,∴∠ABG=∠AGB,∠CBG=∠FGB,∴∠GBC=∠BGF.
又∵BC=GF,∴∠BCF=∠GFC.
又∵∠CBG+∠FGB+∠BCF+∠GFC=360°,∴∠CBG+∠BCF=180°,即BG∥CF;
②续①又∵AB∥PC,AG∥PF,∴∠ABG=∠PCF,∠AGB=∠PFC即△ABG∽△PCF;
③续②连接AP交GF的延长线于Q1,交BC的延长线于Q2,则![]() =
=![]() =
=![]() ,而AB=AG,PC=PF,∴
,而AB=AG,PC=PF,∴![]() =
=![]() ,亦有
,亦有![]() =
=![]() ,Q1P=Q2P,∴Q1,Q2重合,即BC,AP,GF相交于点Q,△ABG与△PCF位似.
,Q1P=Q2P,∴Q1,Q2重合,即BC,AP,GF相交于点Q,△ABG与△PCF位似.
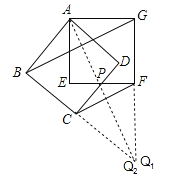
(3)连接AC,AF,CF.
∵ABCD和AEFG都是正方形,∴CA=![]() AB,AF=
AB,AF=![]() AE,∠BAC=∠EAF=45°,∴AC:AF=
AE,∠BAC=∠EAF=45°,∴AC:AF=![]() AB:
AB:![]() AE=AB:AE,∠BAE=∠CAF,∴△ABE∽△ACF,
AE=AB:AE,∠BAE=∠CAF,∴△ABE∽△ACF,![]() =
=![]() .
.


 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案科目:初中数学 来源: 题型:
【题目】(本小题满分8分)某商家预测一种应季衬衫能畅销市场,就用13200元购进了一批这种衬衫,面市后果然供不应求.商家又用28800元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了10元.
(1)该商家购进的第一批衬衫是多少件?
(2)若两批衬衫按相同的标价销售,最后剩下50件按八折优惠卖出,如果两批衬衫全部售完后利润率不低于25%(不考虑其它因素),那么每件衬衫的标价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】东明商场日用品柜台![]() 名售货员
名售货员![]() 月完成的销售额情况如下表:
月完成的销售额情况如下表:
![]()
①计算销售额的平均数、中位数、众数.
②商场为了完成年度的销售任务,调动售货员的积极性,在一年的最后月份采取超额有奖的办法.你认为根据上面计算结果,每个售货员统一的销售额标准是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠B=32°,将△ABC沿直线m翻折,点B落在点D的位置,则∠1-∠2的度数是( )
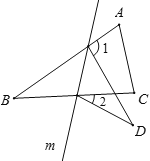
A. 32° B. 64° C. 65° D. 70°
查看答案和解析>>
科目:初中数学 来源: 题型:
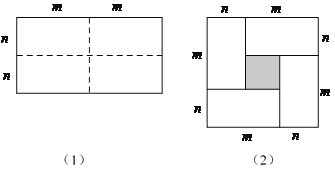
【题目】如图(1)是一个长为2m,宽为2n的长方形,沿图中虚线剪成四个均匀的小长方形,然后按图(2)形状拼成一个正方形.
(1)你认为图(2)中的阴影部分的正方形的边长等于多少?
(2)观察图(2),你能写出下列三个代数式之间的等量关系吗?代数式:![]() ,
,![]() ,
,![]() ;
;
(3)已知:![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把矩形纸片ABCD沿EF翻折,点A恰好落在BC边的A′处,若AB= ![]() ,∠EFA=60°,则四边形A′B′EF的周长是( )
,∠EFA=60°,则四边形A′B′EF的周长是( )

A. 1+3![]() B. 3+
B. 3+![]() C. 4+
C. 4+![]() D. 5+
D. 5+![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ADB、△BCD都是等边三角形,点E,F分别是AB,AD上两个动点,满足AE=DF.连接BF与DE相交于点G,CH⊥BF,垂足为H,连接CG.若DG=![]() ,BG=
,BG=![]() ,且
,且![]() 、
、![]() 满足下列关系:
满足下列关系:![]() ,
,![]() ,则GH= .
,则GH= .

查看答案和解析>>
科目:初中数学 来源: 题型:
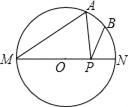
【题目】如图,MN是⊙O的直径,∠AMN=40°,点B为弧AN的中点,点P是直径MN上的一个动点,如果PA+PB的最小值为![]() ,那么⊙O的直径等于( )
,那么⊙O的直径等于( )
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
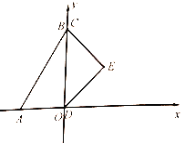
【题目】在平面直角坐标系中,一副含![]() 和
和![]() 角的三角板
角的三角板![]() 和
和![]() 如图摆放,边
如图摆放,边![]() 与
与![]() 重合,
重合,![]() .当点
.当点![]() 从点
从点![]() 出发沿
出发沿![]() 方向滑动时,点
方向滑动时,点![]() 同时从点
同时从点![]() 出发沿
出发沿![]() 轴正方向滑动.
轴正方向滑动.
![]() 设点
设点![]() 关于
关于![]() 的函数表达式为________.
的函数表达式为________.
![]() 连接
连接![]() .当点
.当点![]() 从点
从点![]() 滑动到点
滑动到点![]() 时,
时,![]() 的面积最大值为_______.
的面积最大值为_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com