
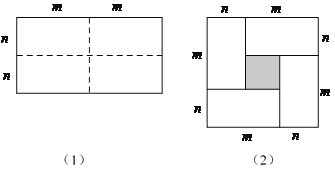
【题目】如图(1)是一个长为2m,宽为2n的长方形,沿图中虚线剪成四个均匀的小长方形,然后按图(2)形状拼成一个正方形.
(1)你认为图(2)中的阴影部分的正方形的边长等于多少?
(2)观察图(2),你能写出下列三个代数式之间的等量关系吗?代数式:![]() ,
,![]() ,
,![]() ;
;
(3)已知:![]() ,
,![]() ,求
,求![]() 的值.
的值.
 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案科目:初中数学 来源: 题型:
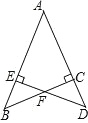
【题目】如图,△ABC,△ADE 均是等腰直角三角形,BC 与 DE 相交于 F 点,若 AC=AE=1,则四边形 AEFC 的周长为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,△ABC的面积为84,BC=21,现将△ABC沿直线BC向右平移a(0<a<21)个单位到△DEF的位置.
(1)求BC边上的高;
(2)若AB=10,
①求线段DF的长;
②连结AE,当△ABE时等腰三角形时,求a的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一长方形花园用来种植菊花和郁金香,其余作为休息区;
(1)求种植菊花和郁金香的面积;
(2)当![]() m,
m,![]() m时,种植菊花和郁金香的面积是多少m2?
m时,种植菊花和郁金香的面积是多少m2?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:
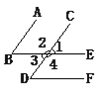
(1)如果∠1=∠B,那么_______∥_______,根据是__________________________;
(2)如果∠3=∠D,那么_______∥_______,根据是__________________________;
(3)如果要使BE∥DF,必须∠1=∠_______,根据是_________________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为迎接五月份全县中考九年级体育测试,小强每天坚持引体向上锻炼,他记录了某一周每天做引体向上的个数,如下表: 
其中有三天的个数被墨汁覆盖了,但小强已经计算出这组数据唯一众数是13,平均数是12,那么这组数据的方差是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,四边形 ABCD,∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m.
(1)求证:BD⊥CB;
(2)求四边形 ABCD 的面积;
(3)如图 2,以 A 为坐标原点,以 AB、AD所在直线为 x轴、y轴建立直角坐标系,
点P在y轴上,若 S△PBD=![]() S四边形ABCD,求 P的坐标.
S四边形ABCD,求 P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠B=90°,∠A=30°,以点A为圆心,BC长为半径画弧交AB于点D,分别以点A、D为圆心,AB长为半径画弧,两弧交于点E,连接AE,DE,则∠EAD的余弦值是( ) 
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y= ![]() x2﹣
x2﹣ ![]() x+c与y轴交于点A(0,﹣
x+c与y轴交于点A(0,﹣ ![]() ),与x轴交于B、C两点,其对称轴与x轴交于点D,直线l∥AB且过点D.
),与x轴交于B、C两点,其对称轴与x轴交于点D,直线l∥AB且过点D.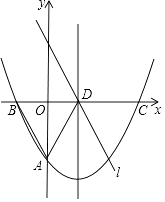
(1)求AB所在直线的函数表达式;
(2)请你判断△ABD的形状并证明你的结论;
(3)点E在线段AD上运动且与点A、D不重合,点F在直线l上运动,且∠BEF=60°,连接BF,求出△BEF面积的最小值.
解:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com