
【题目】如图所示,四边形 ABCD,∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m.
(1)求证:BD⊥CB;
(2)求四边形 ABCD 的面积;
(3)如图 2,以 A 为坐标原点,以 AB、AD所在直线为 x轴、y轴建立直角坐标系,
点P在y轴上,若 S△PBD=![]() S四边形ABCD,求 P的坐标.
S四边形ABCD,求 P的坐标.

【答案】(1)证明见解析;(2)36m2;(3)P 的坐标为(0,-2)或(0,10).
【解析】
(1)先根据勾股定理求出 BD 的长度,然后根据勾股定理的逆定理,即可证明
BD⊥BC;
(2)根据四边形 ABCD 的面积=△ABD 的面积+△BCD 的面积,代入数据计算即可求解;
(3)先根据 S△PBD=![]() S四边形 ABCD,求出 PD,再根据 D 点的坐标即可求解.
S四边形 ABCD,求出 PD,再根据 D 点的坐标即可求解.
(1)证明:连接 BD.
∵AD=4m,AB=3m,∠BAD=90°,
∴BD=5m.
又∵BC=12m,CD=13m,
∴BD2+BC2=CD2.
∴BD⊥CB;
(2)四边形 ABCD 的面积=△ABD 的面积+△BCD 的面积
=![]() ×3×4+
×3×4+ ![]() ×12×5
×12×5
=6+30
=36(m2).
故这块土地的面积是 36m2;
(3)∵S△PBD=![]() S 四边形ABCD
S 四边形ABCD
∴![]() PDAB=
PDAB=![]() ×36,
×36,
∴![]() PD×3=9,
PD×3=9,
∴PD=6,
∵D(0,4),点 P 在 y 轴上,
∴P 的坐标为(0,-2)或(0,10).


科目:初中数学 来源: 题型:
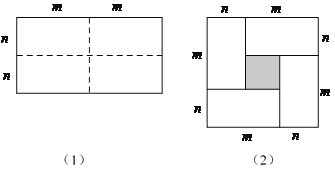
【题目】如图(1)是一个长为2m,宽为2n的长方形,沿图中虚线剪成四个均匀的小长方形,然后按图(2)形状拼成一个正方形.
(1)你认为图(2)中的阴影部分的正方形的边长等于多少?
(2)观察图(2),你能写出下列三个代数式之间的等量关系吗?代数式:![]() ,
,![]() ,
,![]() ;
;
(3)已知:![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】植树节期间,某单位欲购进A、B两种树苗,若购进A种树苗3棵,B种树苗5棵,需2100元,若购进A种树苗4棵,B种树苗10棵,需3800元.
(1)求购进A、B两种树苗的单价;
(2)若该单位准备用不多于8000元的钱购进这两种树苗共30棵,求A种树苗至少需购进多少棵?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】京九铁路是1992年10月全线开工,1996年9月1日建成通车,是中国一次性建成双线线路最长的一项宏伟铁路工程.其中北京﹣商丘段全长约800千米,京九铁路的通车使商丘成为河南省仅次于郑州的第二大枢纽城市,为商丘提供了发展的机遇.京雄商高铁的预设平均速度将是老京九铁路速度的3倍,可以提前5.8个小时从北京到达商丘,求京雄高铁的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2018次运动后,动点P的坐标是_____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于数轴上不重合的两点A,B,给出如下定义:若数轴上存在一点M,通过比较线段AM和BM的长度,将较短线段的长度定义为点M到线段AB的“绝对距离”. 若线段AM和BM的长度相等,将线段AM或BM的长度定义为点M到线段AB的“绝对距离”.
(1)当数轴上原点为O,点A表示的数为-1,点B表示的数为5时.
①点O到线段AB的“绝对距离”为____;
②点M表示的数为![]() ,若点M到线段AB的“绝对距离”为3,则
,若点M到线段AB的“绝对距离”为3,则![]() 的值为______;
的值为______;
(2)在数轴上,点P表示的数为-6,点A表示的数为-3,点B表示的数为2. 点P以每秒2个单位长度的速度向正半轴方向移动时,点B同时以每秒1个单位长度的速度向负半轴方向移动. 设移动的时间为![]() 秒,当点P到线段AB的“绝对距离”为2时,求
秒,当点P到线段AB的“绝对距离”为2时,求![]() 的值.
的值.
![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com