
【题目】对于数轴上不重合的两点A,B,给出如下定义:若数轴上存在一点M,通过比较线段AM和BM的长度,将较短线段的长度定义为点M到线段AB的“绝对距离”. 若线段AM和BM的长度相等,将线段AM或BM的长度定义为点M到线段AB的“绝对距离”.
(1)当数轴上原点为O,点A表示的数为-1,点B表示的数为5时.
①点O到线段AB的“绝对距离”为____;
②点M表示的数为![]() ,若点M到线段AB的“绝对距离”为3,则
,若点M到线段AB的“绝对距离”为3,则![]() 的值为______;
的值为______;
(2)在数轴上,点P表示的数为-6,点A表示的数为-3,点B表示的数为2. 点P以每秒2个单位长度的速度向正半轴方向移动时,点B同时以每秒1个单位长度的速度向负半轴方向移动. 设移动的时间为![]() 秒,当点P到线段AB的“绝对距离”为2时,求
秒,当点P到线段AB的“绝对距离”为2时,求![]() 的值.
的值.
![]()
【答案】(1)①1;②4或 2或 8;(2)![]() 或
或![]() .
.
【解析】
(1)根据绝对距离的含义分类讨论列方程即可,(2)分类讨论, 当![]() 时或当
时或当![]() 时,列方程求解即可.
时,列方程求解即可.
解:(1) 1;
理由:∵点A表示的数为-1,点B表示的数为5,
∴OA=1,OB=5,
∵1![]() 5,
5,
∴点O到线段AB的“绝对距离”为1,
4或 2或 8;
理由:分三种情况;
当点M在A的左侧时,此时m![]() -1, 点M到线段AB的“绝对距离”=-1-m=3,解得:m=-4,
-1, 点M到线段AB的“绝对距离”=-1-m=3,解得:m=-4,
当点M在A,B之间时, 此时![]() m
m![]() 5, 点M到线段AB的“绝对距离”=m+1=3或5-m=3,解得两个方程的答案都是m=2,
5, 点M到线段AB的“绝对距离”=m+1=3或5-m=3,解得两个方程的答案都是m=2,
当点M在B的右侧时,此时m![]() 5, 点M到线段AB的“绝对距离”=m-5=3,解得:m=8,
5, 点M到线段AB的“绝对距离”=m-5=3,解得:m=8,
综上,![]() 的值为4或 2或 8.
的值为4或 2或 8.
(2)当![]() 时, 可得
时, 可得![]() ,解得
,解得![]() ,
,
而当![]() 时,
时,![]() ,
,![]() <
<![]() ,点P到线段AB的“绝对距离”为
,点P到线段AB的“绝对距离”为![]() ,不符合题意.
,不符合题意.
所以![]() .
.
当![]() 时, 可得
时, 可得![]() ,解得
,解得![]() ,而当
,而当![]()
时,![]() ,
,![]() >
>![]() ,点P到线段AB的“绝对距离”1,不符合题意.
,点P到线段AB的“绝对距离”1,不符合题意.
所以![]() .
.
综上所述,所以![]() 或
或![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图所示,四边形 ABCD,∠A=90°,AB=3m,BC=12m,CD=13m,DA=4m.
(1)求证:BD⊥CB;
(2)求四边形 ABCD 的面积;
(3)如图 2,以 A 为坐标原点,以 AB、AD所在直线为 x轴、y轴建立直角坐标系,
点P在y轴上,若 S△PBD=![]() S四边形ABCD,求 P的坐标.
S四边形ABCD,求 P的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列两个等式:3+2=3×2-1,4+![]() =4×
=4×![]() -1,给出定义如下:
-1,给出定义如下:
我们称使等式a+b=ab-1成立的一对有理数a,b为“椒江有理数对”,记为(a,b),如:数对(3,2),(4,![]() )都是“椒江有理数对”.
)都是“椒江有理数对”.
(1)数对(-2,1),(5,![]() )中是“椒江有理数对”的是 ;
)中是“椒江有理数对”的是 ;
(2)若(a,3)是“椒江有理数对”,求a的值;
(3)若(m,n)是“椒江有理数对”,则(-n,-m) “椒江有理数对”(填“是”、“不是”或“不确定”).
(4)请再写出一对符合条件的“椒江有理数对” (注意:不能与题目中已有的“椒江有理数对”重复)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y= ![]() x2﹣
x2﹣ ![]() x+c与y轴交于点A(0,﹣
x+c与y轴交于点A(0,﹣ ![]() ),与x轴交于B、C两点,其对称轴与x轴交于点D,直线l∥AB且过点D.
),与x轴交于B、C两点,其对称轴与x轴交于点D,直线l∥AB且过点D.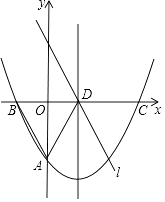
(1)求AB所在直线的函数表达式;
(2)请你判断△ABD的形状并证明你的结论;
(3)点E在线段AD上运动且与点A、D不重合,点F在直线l上运动,且∠BEF=60°,连接BF,求出△BEF面积的最小值.
解:
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学活动课上,老师准备了若干个如图1的三种纸片,A种纸片边长为a的正方形,B种纸片是边长为b的正方形,C种纸片长为a、宽为b的长方形.并用A种纸片一张,B种纸片张,C种纸片两张拼成如图2的大正方形.
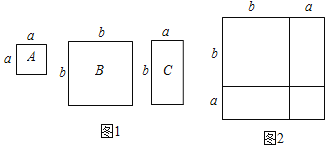
(1)请用两种不同的方法求图2大正方形的面积.
方法1: ;方法2:
(2)观察图2,请你写出下列三个代数式:(a+b)2,a2+b2,ab之间的等量关系.
(3)根据(2)题中的等量关系,解决如下问题:
①已知:a+b=5,a2+b2=11,求ab的值;
②已知(2018﹣a)2+(a﹣2017)2=5,求(2018﹣a)(a﹣2017)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解方程:![]() -
-![]() =1-
=1-![]()
解:去分母,得_________________________________.
去括号,得___________________________.
移项,得___________________________.
合并同类项,得__________.
两边都除以______,得x=_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
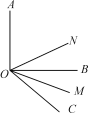
【题目】(1)如图,∠AOB=90°,∠BOC=40°,ON平分∠AOC,OM平分∠BOC,求∠MON的度数;
(2)如果(1)中∠BOC=α,且α<90°,其他条件不变,求∠MON的度数;
(3)如果(1)中∠AOB=β,且β<90°,其他条件不变,求∠MON的度数;
(4)从(1)(2)(3)的结果中能得到什么规律?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料.
点M,N在数轴上分别表示数m和n,我们把m,n之差的绝对值叫做点M,N之间的距离,即MN=|m﹣n|.如图,在数轴上,点A,B,O,C,D的位置如图所示,则DC=|3﹣1|=|2|=2;CO=|1﹣0|=|1|=1;BC=|(﹣2)﹣1|=|﹣3|=3;AB=|(﹣4)﹣(﹣2)|=|﹣2|=2.
![]()
(1)OA= ,BD= ;
(2)|1﹣(﹣4)|表示哪两点的距离?
(3)点P为数轴上一点,其表示的数为x,用含有x的式子表示BP= ,当BP=4时,x= ;当|x﹣3|+|x+2|的值最小时,x的取值范围是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于实数a,我们规定:用符号[![]() ]表示不大于
]表示不大于![]() 的最大整数,称[
的最大整数,称[![]() ]为a的根整数,例如:[
]为a的根整数,例如:[![]() ]=3,[
]=3,[![]() ]=3.
]=3.
(1)仿照以上方法计算:[![]() ] = ;[
] = ;[![]() ] = .
] = .
(2)若[![]() ]=1,写出满足题意的x的整数值 .
]=1,写出满足题意的x的整数值 .
如果我们对a连续求根整数,直到结果为1为止.例如:对10连续求根整数2次 [![]() ]=3→[
]=3→[![]() ]=1,这时候结果为1.
]=1,这时候结果为1.
(3)对100连续求根整数, 次之后结果为1.
(4)只需进行3次连续求根整数运算后结果为1的所有正整数中,最大的是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com