
【题目】观察下列两个等式:3+2=3×2-1,4+![]() =4×
=4×![]() -1,给出定义如下:
-1,给出定义如下:
我们称使等式a+b=ab-1成立的一对有理数a,b为“椒江有理数对”,记为(a,b),如:数对(3,2),(4,![]() )都是“椒江有理数对”.
)都是“椒江有理数对”.
(1)数对(-2,1),(5,![]() )中是“椒江有理数对”的是 ;
)中是“椒江有理数对”的是 ;
(2)若(a,3)是“椒江有理数对”,求a的值;
(3)若(m,n)是“椒江有理数对”,则(-n,-m) “椒江有理数对”(填“是”、“不是”或“不确定”).
(4)请再写出一对符合条件的“椒江有理数对” (注意:不能与题目中已有的“椒江有理数对”重复)
【答案】(1) (5,![]() );(2)2;(3)不是.(4)(6,1.4)等.
);(2)2;(3)不是.(4)(6,1.4)等.
【解析】
(1)根据“椒江有理数对”的定义即可判断;
(2)根据“椒江有理数对”的定义,构建方程即可解决问题;
(3)根据“椒江有理数对”的定义即可判断;
(4)根据“椒江有理数对”的定义即可解决问题.
(1)-2+1=-1,-2×1-1=-3,
∴-2+1≠-2×1-1,
∴(-2,1)不是“共生有理数对”,
∵5+![]() =
=![]() ,5×
,5×![]() -1=
-1=![]() ,
,
∴5+![]() =5×
=5×![]() -1,
-1,
∴(5,![]() )中是“椒江有理数对”;
)中是“椒江有理数对”;
(2)由题意得:
a+3=3a-1,
解得a=2.
(3)不是.
理由:-n+(-m)=-n-m,
-n(-m)-1=mn-1
∵(m,n)是“椒江有理数对”
∴m+n=mn-1
∴-n-m=-(mn-1)=-(-n)×(-m)+1=-[(-n)×(-m)-1],
∴(-n,-m)不是“椒江有理数对”,
(4)(6,1.4)等.


 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:初中数学 来源: 题型:
【题目】京九铁路是1992年10月全线开工,1996年9月1日建成通车,是中国一次性建成双线线路最长的一项宏伟铁路工程.其中北京﹣商丘段全长约800千米,京九铁路的通车使商丘成为河南省仅次于郑州的第二大枢纽城市,为商丘提供了发展的机遇.京雄商高铁的预设平均速度将是老京九铁路速度的3倍,可以提前5.8个小时从北京到达商丘,求京雄高铁的平均速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,动点P在平面直角坐标系中按图中箭头所示方向运动,第1次从原点运动到点(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过第2018次运动后,动点P的坐标是_____________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1.在菱形ABCD中,AB=2 ![]() ,tan∠ABC=2,∠BCD=α,点E从点D出发,以每秒1个单位长度的速度沿着射线DA的方向匀速运动,设运动时间为t(秒),将线段CE绕点C顺时针旋转α度,得到对应线段CF,连接BD、EF,BD交EC、EF于点P、Q.
,tan∠ABC=2,∠BCD=α,点E从点D出发,以每秒1个单位长度的速度沿着射线DA的方向匀速运动,设运动时间为t(秒),将线段CE绕点C顺时针旋转α度,得到对应线段CF,连接BD、EF,BD交EC、EF于点P、Q.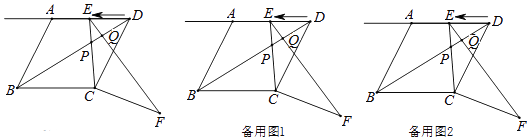
(1)求证:△ECF∽△BCD;
(2)当t为何值时,△ECF≌△BCD?
(3)当t为何值时,△EPQ是直角三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,∠A=140°,∠D=80°.

(1)如图1,若∠B=∠C,试求出∠C的度数;
(2)如图2,若∠ABC的角平分线BE交DC于点E,且BE∥AD,试求出∠C的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于数轴上不重合的两点A,B,给出如下定义:若数轴上存在一点M,通过比较线段AM和BM的长度,将较短线段的长度定义为点M到线段AB的“绝对距离”. 若线段AM和BM的长度相等,将线段AM或BM的长度定义为点M到线段AB的“绝对距离”.
(1)当数轴上原点为O,点A表示的数为-1,点B表示的数为5时.
①点O到线段AB的“绝对距离”为____;
②点M表示的数为![]() ,若点M到线段AB的“绝对距离”为3,则
,若点M到线段AB的“绝对距离”为3,则![]() 的值为______;
的值为______;
(2)在数轴上,点P表示的数为-6,点A表示的数为-3,点B表示的数为2. 点P以每秒2个单位长度的速度向正半轴方向移动时,点B同时以每秒1个单位长度的速度向负半轴方向移动. 设移动的时间为![]() 秒,当点P到线段AB的“绝对距离”为2时,求
秒,当点P到线段AB的“绝对距离”为2时,求![]() 的值.
的值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:△ABC是边长为4的等边三角形,点O在边AB上,⊙O过点B且分别与边AB,BC相交于点D,E,EF⊥AC,垂足为F.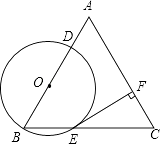
(1)求证:直线EF是⊙O的切线;
(2)当直线DF与⊙O相切时,求⊙O的半径.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com