
【题目】数学活动课上,老师准备了若干个如图1的三种纸片,A种纸片边长为a的正方形,B种纸片是边长为b的正方形,C种纸片长为a、宽为b的长方形.并用A种纸片一张,B种纸片张,C种纸片两张拼成如图2的大正方形.
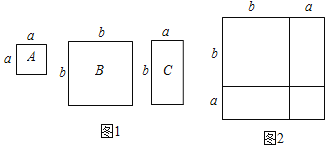
(1)请用两种不同的方法求图2大正方形的面积.
方法1: ;方法2:
(2)观察图2,请你写出下列三个代数式:(a+b)2,a2+b2,ab之间的等量关系.
(3)根据(2)题中的等量关系,解决如下问题:
①已知:a+b=5,a2+b2=11,求ab的值;
②已知(2018﹣a)2+(a﹣2017)2=5,求(2018﹣a)(a﹣2017)的值.
【答案】(1)(a+b)2,a2+b2+2ab; (2)(a+b)2=a2+2ab+b2;(3)①ab=7 ;② (2018﹣a)(a﹣2017)=﹣2.
【解析】
(1)两个小正方形的面积加上矩形的面积即可得出大正方形的面积或者直接运用大正方形的边长求解即可;
(2)由面积关系容易得出结论;
(3)①根据(2)所得出的关系式,容易求出结果;
②先根据题意得出(2018﹣a)与(a﹣2017)的等量关系,即可得出结果.
(1)(a+b)2,a2+b2+2ab;
(2)(a+b)2=a2+2ab+b2;
(3)① ∵a+b=5,
∴(a+b)2=25,
∴a2+b2+2ab=25,
又∵a2+b2=11,
∴ab=7 ;
② 设2018﹣a=x,a﹣2017=y,则x+y=1,
∵(2018﹣a)2+(a﹣2017)2=5,
∴ x2+y2=5,
∵(x+y)2=x2+2xy+y2,
∴xy=![]() =﹣2,
=﹣2,
即(2018﹣a)(a﹣2017)=﹣2.


 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案科目:初中数学 来源: 题型:
【题目】如图1.在菱形ABCD中,AB=2 ![]() ,tan∠ABC=2,∠BCD=α,点E从点D出发,以每秒1个单位长度的速度沿着射线DA的方向匀速运动,设运动时间为t(秒),将线段CE绕点C顺时针旋转α度,得到对应线段CF,连接BD、EF,BD交EC、EF于点P、Q.
,tan∠ABC=2,∠BCD=α,点E从点D出发,以每秒1个单位长度的速度沿着射线DA的方向匀速运动,设运动时间为t(秒),将线段CE绕点C顺时针旋转α度,得到对应线段CF,连接BD、EF,BD交EC、EF于点P、Q.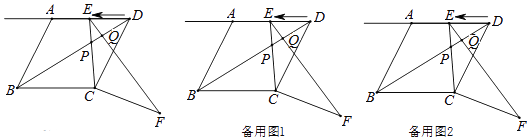
(1)求证:△ECF∽△BCD;
(2)当t为何值时,△ECF≌△BCD?
(3)当t为何值时,△EPQ是直角三角形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,∠A=140°,∠D=80°.

(1)如图1,若∠B=∠C,试求出∠C的度数;
(2)如图2,若∠ABC的角平分线BE交DC于点E,且BE∥AD,试求出∠C的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,射线AM平分∠BAC,AB=8,cos∠ACB= ![]() ,点P为射线AM上一点,且PB=PC,则四边形ABPC的面积为 .
,点P为射线AM上一点,且PB=PC,则四边形ABPC的面积为 . 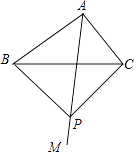
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于数轴上不重合的两点A,B,给出如下定义:若数轴上存在一点M,通过比较线段AM和BM的长度,将较短线段的长度定义为点M到线段AB的“绝对距离”. 若线段AM和BM的长度相等,将线段AM或BM的长度定义为点M到线段AB的“绝对距离”.
(1)当数轴上原点为O,点A表示的数为-1,点B表示的数为5时.
①点O到线段AB的“绝对距离”为____;
②点M表示的数为![]() ,若点M到线段AB的“绝对距离”为3,则
,若点M到线段AB的“绝对距离”为3,则![]() 的值为______;
的值为______;
(2)在数轴上,点P表示的数为-6,点A表示的数为-3,点B表示的数为2. 点P以每秒2个单位长度的速度向正半轴方向移动时,点B同时以每秒1个单位长度的速度向负半轴方向移动. 设移动的时间为![]() 秒,当点P到线段AB的“绝对距离”为2时,求
秒,当点P到线段AB的“绝对距离”为2时,求![]() 的值.
的值.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b的图象与反比例函数y= ![]() (x>0)的图象交于点P(n,2),与x轴交于点A(﹣4,0),与y轴交于点C,PB⊥x轴于点B,点A与点B关于y轴对称.
(x>0)的图象交于点P(n,2),与x轴交于点A(﹣4,0),与y轴交于点C,PB⊥x轴于点B,点A与点B关于y轴对称.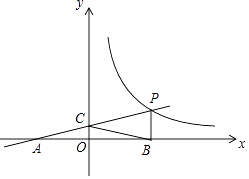
(1)求一次函数,反比例函数的解析式;
(2)求证:点C为线段AP的中点;
(3)反比例函数图象上是否存在点D,使四边形BCPD为菱形?如果存在,说明理由并求出点D的坐标;如果不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:二次函数y=ax2+bx+c的图象所示,下列结论中:①abc>0;②2a+b=0;③当m≠1时,a+b>am2+bm;④a﹣b+c>0;⑤若ax12+bx1=ax22+bx2 , 且x1≠x2 , 则x1+x2=2,正确的个数为( ) 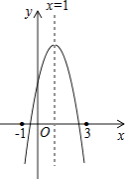
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com