
【题目】如图,在△ABC中,∠BAC=90°,射线AM平分∠BAC,AB=8,cos∠ACB= ![]() ,点P为射线AM上一点,且PB=PC,则四边形ABPC的面积为 .
,点P为射线AM上一点,且PB=PC,则四边形ABPC的面积为 . 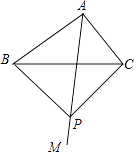
【答案】49
【解析】解:∵在△ABC中,∠BAC=90°,AB=8,cos∠ACB= ![]() , ∴设AC=3k,BC=5k,
, ∴设AC=3k,BC=5k,
∴AB=4k,
∴k=2,
∴BC=10,AC=6,
过P作PE⊥AB于E,PF⊥于F,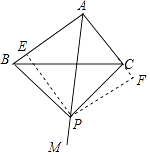
∴四边形AEPF是矩形,
∵射线AM平分∠BAC,
∴PE=PF,
∴矩形AEPF是正方形,
在Rt△PBE与Rt△PFC中 ![]() ,
,
∴Rt△PBE≌Rt△PFC,
∴BE=CF,
∴AE=AF=7,
∴四边形ABPC的面积=正方形AEPF的面积=7×7=49,
所以答案是:49.
【考点精析】认真审题,首先需要了解角平分线的性质定理(定理1:在角的平分线上的点到这个角的两边的距离相等; 定理2:一个角的两边的距离相等的点,在这个角的平分线上),还要掌握解直角三角形(解直角三角形的依据:①边的关系a2+b2=c2;②角的关系:A+B=90°;③边角关系:三角函数的定义.(注意:尽量避免使用中间数据和除法))的相关知识才是答题的关键.


 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案科目:初中数学 来源: 题型:
【题目】十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式,被称为欧拉公式.请你观察下列几种简单的多面体模型,解答下列问题:
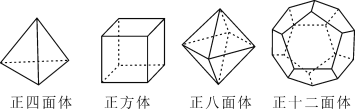
(1)根据上面的多面体模型,完成表格:
多面体 | 顶点数(V) | 面数(F) | 棱数(E) |
四面体 | 4 | 4 | |
正方体 | 8 | 12 | |
正八面体 | 6 | 8 | 12 |
正十二面体 | 20 | 12 | 30 |
可以发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是_______________;
(2)若一个多面体的面数比顶点数大8,且有30条棱,则这个多面体的面数是______;
(3)某个玻璃饰品的外形是简单多面体,它的外表面是由三角形和八边形两种多边形拼接而成,且有24个顶点,每个顶点处有3条棱.设该多面体外表面三角形的个数为x,八边形的个数为y,求x+y的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中的△ABC,若小方格边长为1,格点△ABC(顶点是网格线交点的三角形)的顶点A,C的坐标分别为(﹣1,1),(0,﹣2),请你根据所学的知识.
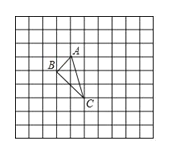
(1)在如图所示的网格平面内作出平面直角坐标系;
(2)作出△ABC关于y轴对称的三角形A1B1C1;
(3)判断△ABC的形状,并求出△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径是2,AB是⊙O的弦,点P是弦AB上的动点,且1≤OP≤2,则弦AB所对的圆周角的度数是( ) 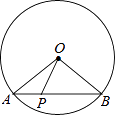
A.60°
B.120°
C.60°或120°
D.30°或150°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学活动课上,老师准备了若干个如图1的三种纸片,A种纸片边长为a的正方形,B种纸片是边长为b的正方形,C种纸片长为a、宽为b的长方形.并用A种纸片一张,B种纸片张,C种纸片两张拼成如图2的大正方形.
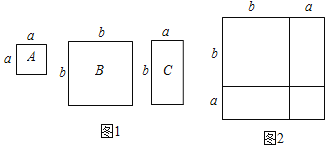
(1)请用两种不同的方法求图2大正方形的面积.
方法1: ;方法2:
(2)观察图2,请你写出下列三个代数式:(a+b)2,a2+b2,ab之间的等量关系.
(3)根据(2)题中的等量关系,解决如下问题:
①已知:a+b=5,a2+b2=11,求ab的值;
②已知(2018﹣a)2+(a﹣2017)2=5,求(2018﹣a)(a﹣2017)的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校数学综合实践小组的同学以“绿色出行”为主题,把某小区的居民对共享单车的了解和使用情况进行了问卷调查,在这次调查中,发现有20人对于共享单车不了解,使用共享单车的居民每天骑行路程不超过8千米,并将调查结果制作成统计图,如图所示. 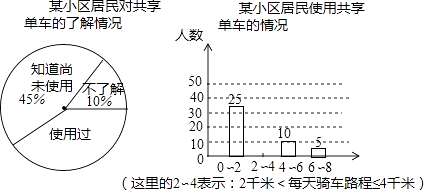
(1)本次调查人数共人 , 使用过共享单车的有人;
(2)请将条形统计图补充完整;
(3)如果这个小区大约有3000名居民,请估算出每天的骑行路程在2~4千米的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线l1∥l2,且l3和l1,l2分别交于A,B两点,点P在AB上.
(1)试找出∠1,∠2,∠3之间的关系并说出理由;
(2)如果点P在A,B两点之间运动,问∠1,∠2,∠3之间的关系是否发生变化?
(3)如果点P在A,B两点外侧运动,试探究∠1,∠2,∠3之间的关系(点P和A,B不重合).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“道路交通管理条例”规定:小汽车在城街上行驶速度不得超过70千米/小时,如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路面对车速检测仪A正前方30米B处,过了2秒后,测得小汽车C与车速检测仪A间距离为50米,这辆小汽车超速了吗?
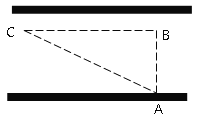
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com