
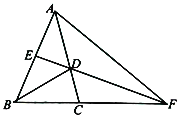
【题目】如图,在△ABC中,AB=AC,∠A=36°,BD是∠B的平分线,交AC于点D,E是AB中点,ED交BC的延长线于点F.求证:AB=CF.
【答案】见解析
【解析】
根据等腰三角形的性质,可得∠ABC=∠ACB=72°,根据角平分线的性质,可得∠1=∠2=36°,可得DA与DB的关系,根据线段垂直平分线的判定与性质,可得FA与FB的关系,可得∠FAB与∠ABC的关系,根据三角形外角的关系,可得∠AFC=∠ACB-∠3=36°,根据等腰三角形的判定,可得AC与CF的关系,根据等量代换,可得答案.
证明:如图,连接AF,
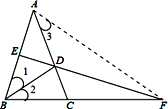
∵AB=AC,∠BAC=36°,
∴∠ABC=∠ACB=72°.
∵BD平分∠ABC,
∴∠1=∠2=36°,
∴∠1=∠BAD=36°,
∴DA=DB.
∵AE=BE,
∴FE⊥AB,即FE是AB的垂直平分线,
∴FA=FB,
∴∠FAB=∠ABC=72°,
∴∠3=∠FAB-∠BAC=36°,
∵∠ACB=∠3+∠AFC,
∴∠AFC=∠ACB-∠3=36°,
∴∠3=∠AFC,
∴AC=CF,
∴AB=CF.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),B(4,0),与y轴交于点C(0,2),点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l,交抛物线于点Q.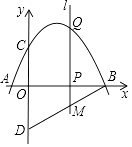
(1)求抛物线的解析式;
(2)求直线BD的解析式;
(3)当点P在线段OB上运动时,直线l交BD于点M,是否存在点P,使得四边形CQMD是平行四边形?若存在,求出m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义[a,b,c]为函数y=ax2+bx+c的特征数,下面给出特征数为[2m,1﹣m,﹣1﹣m]的函数的一些结论,其中不正确的是( )
A.当m=﹣3时,函数图象的顶点坐标是( ![]() )
)
B.当m>0时,函数图象截x轴所得的线段长度大于 ![]()
C.当m≠0时,函数图象经过同一个点
D.当m<0时,函数在x ![]() 时,y随x的增大而减小
时,y随x的增大而减小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答题
(1)如图1,AD、BC相交于点O,OA=OC,∠OBD=∠ODB.求证:AB=CD. 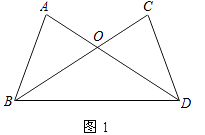
(2)如图2,AB是⊙O的直径,OA=1,AC是⊙O的弦,过点C的切线交AB的延长线于点D,若OD= ![]() ,求∠BAC的度数.
,求∠BAC的度数. 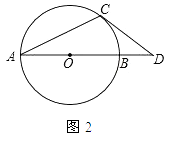
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,P为平行四边形ABCD的边AD上的一点,E,F分别为PB,PC的中点,△PEF,△PDC,△PAB的面积分别为S,S1 , S2 . 若S=3,则S1+S2的值为( ) 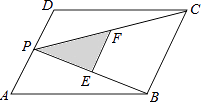
A.24
B.12
C.6
D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,射线AM平分∠BAC,AB=8,cos∠ACB= ![]() ,点P为射线AM上一点,且PB=PC,则四边形ABPC的面积为 .
,点P为射线AM上一点,且PB=PC,则四边形ABPC的面积为 . 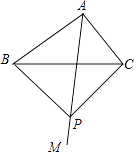
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在植树节到来之际,某小区计划购进A、B两种树苗共17棵,已知A种树苗每棵80元,B种树苗每棵60元.
(1)若购进A、B两种树苗刚好用去1220元,问购进A、B两种树苗各多少棵?
(2)若购买B种树苗的数量少于A种树苗的数量,请你给出一种费用最省的方案,并求出该方案所需费用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A、B两个小集镇在河流CD的同侧,分别到河的距离为AC=10千米,BD=30千米,且CD=30千米,现在要在河边建一自来水厂,向A、B两镇供水,铺设水管的费用为每千米3万,请你在河流CD上选择水厂的位置M,使铺设水管的费用最节省,并求出总费用是多少?
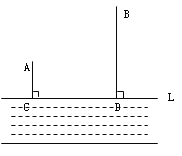
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com