
【题目】定义[a,b,c]为函数y=ax2+bx+c的特征数,下面给出特征数为[2m,1﹣m,﹣1﹣m]的函数的一些结论,其中不正确的是( )
A.当m=﹣3时,函数图象的顶点坐标是( ![]() )
)
B.当m>0时,函数图象截x轴所得的线段长度大于 ![]()
C.当m≠0时,函数图象经过同一个点
D.当m<0时,函数在x ![]() 时,y随x的增大而减小
时,y随x的增大而减小
【答案】D
【解析】解:因为函数y=ax2+bx+c的特征数为[2m,1﹣m,﹣1﹣m]; A、当m=﹣3时,y=﹣6x2+4x+2=﹣6(x﹣ ![]() )2+
)2+ ![]() ,顶点坐标是(
,顶点坐标是( ![]() ,
, ![]() );此结论正确;
);此结论正确;
B、当m>0时,令y=0,有2mx2+(1﹣m)x+(﹣1﹣m)=0,解得:x1=1,x2=﹣ ![]() ﹣
﹣ ![]() ,
,
|x2﹣x1|= ![]() +
+ ![]() >
> ![]() ,所以当m>0时,函数图象截x轴所得的线段长度大于
,所以当m>0时,函数图象截x轴所得的线段长度大于 ![]() ,此结论正确;
,此结论正确;
C、当x=1时,y=2mx2+(1﹣m)x+(﹣1﹣m)=2m+(1﹣m)+(﹣1﹣m)=0 即对任意m,函数图象都经过点(1,0)那么同样的:当m=0时,函数图象都经过同一个点(1,0),当m≠0时,函数图象经过同一个点(1,0),故当m≠0时,函数图象经过x轴上一个定点此结论正确.
D、当m<0时,y=2mx2+(1﹣m)x+(﹣1﹣m) 是一个开口向下的抛物线,其对称轴是: ![]() ,在对称轴的右边y随x的增大而减小.因为当m<0时,
,在对称轴的右边y随x的增大而减小.因为当m<0时, ![]() =
= ![]() ﹣
﹣ ![]() >
> ![]() ,即对称轴在x=
,即对称轴在x= ![]() 右边,因此函数在x=
右边,因此函数在x= ![]() 右边先递增到对称轴位置,再递减,此结论错误;
右边先递增到对称轴位置,再递减,此结论错误;
根据上面的分析,①②③都是正确的,④是错误的.
故选D.
【考点精析】本题主要考查了二次函数的性质的相关知识点,需要掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小才能正确解答此题.


科目:初中数学 来源: 题型:
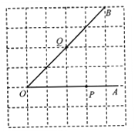
【题目】如图,点P,Q分别是∠AOB的边OA,OB上的点.
(1)过点P画OB的垂线,垂足为H;
(2)过点Q画OA的垂线,交OA于点C,连接PQ;
(3)线段QC的长度是点Q到 的距离, 的长度是点P到直线OB的距离,因为直线外一点和直线上各点连接的所有线段中,垂线段最短,所以线段PQ、PH的大小关系是 (用“<”号连接).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,∠BAC=90°,点D是直线AB上的一动点(不和A、B重合),BE⊥CD于E,交直线AC于F.
(1)点D在边AB上时,请证明:BD=AB﹣AF;
(2)试探索:点D在AB的延长线或反向延长线上时,请在备用图中画出图形,(1)中的结论是否成立?若不成立,请直接写出正确结论(不需要证明).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将正方形OABC放在平面直角坐标系中,O是原点,A的坐标为(1, ![]() ),则点B的坐标为( )
),则点B的坐标为( ) 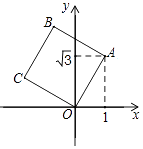
A.(1﹣ ![]() ,
, ![]() +1)
+1)
B.(﹣ ![]() ,
, ![]() +1)??
+1)??
C.(﹣1, ![]() +1)
+1)
D.(﹣1, ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线分别交AB,AC于点D,E.
(1)若∠A=40°,求∠EBC的度数;
(2)若AD=5,△EBC的周长为16,求△ABC的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中的△ABC,若小方格边长为1,格点△ABC(顶点是网格线交点的三角形)的顶点A,C的坐标分别为(﹣1,1),(0,﹣2),请你根据所学的知识.
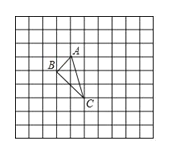
(1)在如图所示的网格平面内作出平面直角坐标系;
(2)作出△ABC关于y轴对称的三角形A1B1C1;
(3)判断△ABC的形状,并求出△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
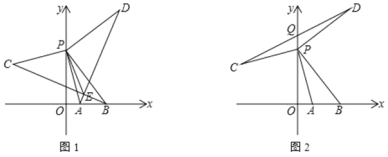
【题目】已知如图,在平面直角坐标系中,点 B(m,0)、A(n,0)分别是 x 轴轴上两点, 且满足多项式(x2+mx+8)(x2-3x+n)的积中不含 x3项和 x2项,点 P(0,h)是 y 轴正半轴上的动点
(1)求三角形△ABP 的面积(用含 h 的代数式表示)
(2)过点 P 作 DP⊥PB,CP⊥PA,且 PD=PB,PC=AP
① 连接 AD、BC 相交于点 E,再连 PE,求∠BEP 的度数
② 连 CD 与 y 轴相交于点 Q,当动点 P 在 y 轴正半轴上运动时,线段 PQ 的长度变不变?如果不变,请求出其值;如果变化,请求出其变化范围
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com