
【题目】如图,将正方形OABC放在平面直角坐标系中,O是原点,A的坐标为(1, ![]() ),则点B的坐标为( )
),则点B的坐标为( ) 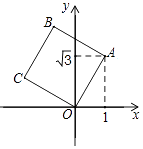
A.(1﹣ ![]() ,
, ![]() +1)
+1)
B.(﹣ ![]() ,
, ![]() +1)??
+1)??
C.(﹣1, ![]() +1)
+1)
D.(﹣1, ![]() )
)
【答案】A
【解析】解:作AE⊥x轴于E,BF⊥EA交EA的延长线于F,BF交y轴于H.则易知四边形OEFH是矩形. 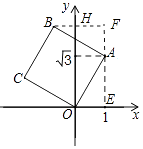
∵四边形ABCO是正方形,A(1, ![]() ),
),
∴AB=AO,∠BAO=90°,AE= ![]() ,HF=OE=1,∠BFA=∠AEO=90°,
,HF=OE=1,∠BFA=∠AEO=90°,
∴∠BAF+∠OAE=90°,∠OAE+∠AOE=90°,
∴∠BAF=∠AOE,
在△BAF和△AOE中,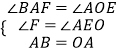 ,
,
∴△BAF≌△AOE,
∴BF=AE= ![]() ,AF=OE=1,
,AF=OE=1,
∴BH= ![]() ﹣1,EF=1+
﹣1,EF=1+ ![]() ,
,
∵B在第三象限,
∴B(1﹣ ![]() ,1+
,1+ ![]() ).
).
故选A.
【考点精析】本题主要考查了正方形的性质的相关知识点,需要掌握正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形才能正确解答此题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c与x轴交于点A(﹣1,0),B(4,0),与y轴交于点C(0,2),点D与点C关于x轴对称,点P是x轴上的一个动点,设点P的坐标为(m,0),过点P作x轴的垂线l,交抛物线于点Q.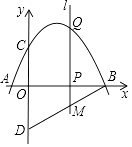
(1)求抛物线的解析式;
(2)求直线BD的解析式;
(3)当点P在线段OB上运动时,直线l交BD于点M,是否存在点P,使得四边形CQMD是平行四边形?若存在,求出m的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A(0,4)是直角坐标系 y 轴上一点,动点 P 从原点 O 出发,沿 x 轴正半轴运动,速度为每秒 1 个单位长度,以P为直角顶点在第一象限内作等腰Rt△APB.设P点的运动时间为 t 秒.
(1)若 AB∥x 轴,求 t 的值;
(2)若OP=![]() OA,求B点的坐标.
OA,求B点的坐标.
(3)当 t=3 时,x 轴上是否存在有一点 M,使得以 M、P、A 为顶点的三角形是等腰三角形,请直接写出点 M 的坐标.
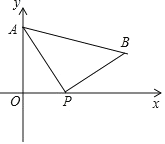
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校组织七年级175名学生参加社会实践活动,已知35座客车的租金为每辆320元,55座客车的租金为每辆400元.
(1)若学校单独租用这两种车,则各需多少元?
(2)若学校同时租用这两种客车共4辆(可以坐不满),而且比单独租用一种车节省租金,请你帮助该学校选择一种最节省租金的租车方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,点A(0,6),B(8,0),AB=10,如图作∠DBO=∠ABO,∠CAy=∠BAO,BD交y轴于点E,直线DO交AC于点C.
(1)①求证:△ACO≌△EDO;②求出线段AC、BD的位置关系和数量关系;
(2)动点P从A出发,沿A﹣O﹣B路线运动,速度为1,到B点处停止运动;动点Q从B出发,沿B﹣O﹣A运动,速度为2,到A点处停止运动.二者同时开始运动,都要到达相应的终点才能停止.在某时刻,作PE⊥CD于点E,QF⊥CD于点F.问两动点运动多长时间时△OPE与△OQF全等?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义[a,b,c]为函数y=ax2+bx+c的特征数,下面给出特征数为[2m,1﹣m,﹣1﹣m]的函数的一些结论,其中不正确的是( )
A.当m=﹣3时,函数图象的顶点坐标是( ![]() )
)
B.当m>0时,函数图象截x轴所得的线段长度大于 ![]()
C.当m≠0时,函数图象经过同一个点
D.当m<0时,函数在x ![]() 时,y随x的增大而减小
时,y随x的增大而减小
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解答题
(1)如图1,AD、BC相交于点O,OA=OC,∠OBD=∠ODB.求证:AB=CD. 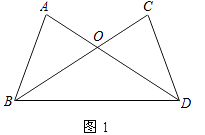
(2)如图2,AB是⊙O的直径,OA=1,AC是⊙O的弦,过点C的切线交AB的延长线于点D,若OD= ![]() ,求∠BAC的度数.
,求∠BAC的度数. 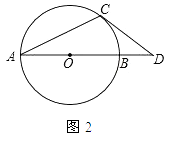
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com