
【题目】解答题
(1)如图1,AD、BC相交于点O,OA=OC,∠OBD=∠ODB.求证:AB=CD. 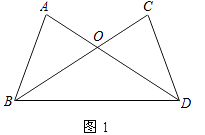
(2)如图2,AB是⊙O的直径,OA=1,AC是⊙O的弦,过点C的切线交AB的延长线于点D,若OD= ![]() ,求∠BAC的度数.
,求∠BAC的度数. 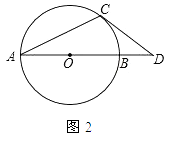
【答案】
(1)证明:∵∠OBD=∠ODB,
∴OB=OD,
在△AOB与△COD中, 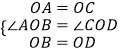 ,
,
∴△AOB≌△COD(SAS),
∴AB=CD
(2)解:连接OC,如图所示:

∵CD与⊙O相切,
∴OC⊥CD,
∵OA=OC,OA=1,
∴OC=1,
∴CD= ![]() =
= ![]() =1,
=1,
∴CD=OC,
∴△OCD为等腰直角三角形,
∴∠COB=45°,
∴∠BAC= ![]() ∠COB=22.5°.
∠COB=22.5°.
【解析】(1)由∠OBD=∠ODB,得出OB=OD,再由SAS证得△AOB≌△COD,即可得出结论;(2)连接OC,由CD与⊙O相切,得出OC⊥CD,求出CD=1,得出△OCD为等腰直角三角形,推出∠COD=45°,即可得出结果.
【考点精析】认真审题,首先需要了解切线的性质定理(切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径).


 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案科目:初中数学 来源: 题型:
【题目】如图,将正方形OABC放在平面直角坐标系中,O是原点,A的坐标为(1, ![]() ),则点B的坐标为( )
),则点B的坐标为( ) 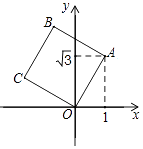
A.(1﹣ ![]() ,
, ![]() +1)
+1)
B.(﹣ ![]() ,
, ![]() +1)??
+1)??
C.(﹣1, ![]() +1)
+1)
D.(﹣1, ![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中的△ABC,若小方格边长为1,格点△ABC(顶点是网格线交点的三角形)的顶点A,C的坐标分别为(﹣1,1),(0,﹣2),请你根据所学的知识.
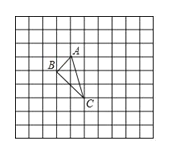
(1)在如图所示的网格平面内作出平面直角坐标系;
(2)作出△ABC关于y轴对称的三角形A1B1C1;
(3)判断△ABC的形状,并求出△ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的半径是2,AB是⊙O的弦,点P是弦AB上的动点,且1≤OP≤2,则弦AB所对的圆周角的度数是( ) 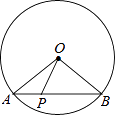
A.60°
B.120°
C.60°或120°
D.30°或150°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校数学综合实践小组的同学以“绿色出行”为主题,把某小区的居民对共享单车的了解和使用情况进行了问卷调查,在这次调查中,发现有20人对于共享单车不了解,使用共享单车的居民每天骑行路程不超过8千米,并将调查结果制作成统计图,如图所示. 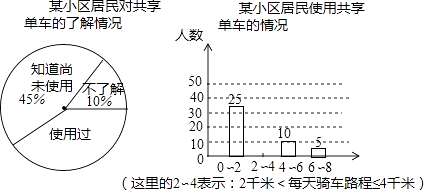
(1)本次调查人数共人 , 使用过共享单车的有人;
(2)请将条形统计图补充完整;
(3)如果这个小区大约有3000名居民,请估算出每天的骑行路程在2~4千米的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
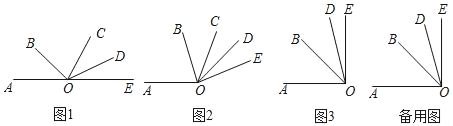
【题目】射线OA、OB、OC、OD、OE有公共端点O.
(1)若OA与OE在同一直线上(如图1),试写出图中小于平角的角;
(2)若∠AOC=108°,∠COE=n°(0<n<72),OB平分∠AOE,OD平分∠COE(如图2),求∠BOD的度数;
(3)如图3,若∠AOE=88°,∠BOD=30°,射OC绕点O在∠AOD内部旋转(不与OA、OD重合).探求:射线OC从OA转到OD的过程中,图中所有锐角的和的情况,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com