
【题目】射线OA、OB、OC、OD、OE有公共端点O.
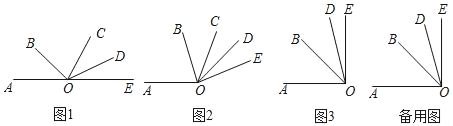
(1)若OA与OE在同一直线上(如图1),试写出图中小于平角的角;
(2)若∠AOC=108°,∠COE=n°(0<n<72),OB平分∠AOE,OD平分∠COE(如图2),求∠BOD的度数;
(3)如图3,若∠AOE=88°,∠BOD=30°,射OC绕点O在∠AOD内部旋转(不与OA、OD重合).探求:射线OC从OA转到OD的过程中,图中所有锐角的和的情况,并说明理由.
【答案】(1)图1中小于平角的角∠AOD,∠AOC,∠AOB,∠BOE,∠BOD,∠BOC,∠COE,∠COD,∠DOE;(2)∠BOD=54°;(3)∠AOE+∠AOB+∠AOC+∠AOD+∠BOC+∠BOD+∠BOE+∠COD+∠COE+∠DOE=412°.理由见解析.
【解析】
(1)根据角的定义即可解决;
(2)利用角平分线的性质即可得出∠BOD=![]() ∠AOC+
∠AOC+![]() ∠COE,进而求出即可;
∠COE,进而求出即可;
(3)将图中所有锐角求和即可求得所有锐角的和与∠AOE、∠BOD和∠BOD的关系,即可解题.
(1)如图1中小于平角的角∠AOD,∠AOC,∠AOB,∠BOE,∠BOD,∠BOC,∠COE,∠COD,∠DOE.

(2)如图2,

∵OB平分∠AOE,OD平分∠COE,∠AOC=108°,∠COE=n°(0<n<72),
∴∠BOD=![]() ∠AOD﹣
∠AOD﹣![]() ∠COE+
∠COE+![]() ∠COE=
∠COE=![]() ×108°=54°;
×108°=54°;
(3)如图3,

∠AOE=88°,∠BOD=30°,
图中所有锐角和为∠AOE+∠AOB+∠AOC+∠AOD+∠BOC+∠BOD+∠BOE+∠COD+∠COE+∠DOE
=4∠AOB+4∠DOE=6∠BOC+6∠COD
=4(∠AOE﹣∠BOD)+6∠BOD
=412°.


科目:初中数学 来源: 题型:
【题目】解答题
(1)如图1,AD、BC相交于点O,OA=OC,∠OBD=∠ODB.求证:AB=CD. 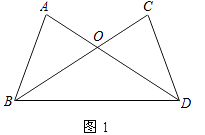
(2)如图2,AB是⊙O的直径,OA=1,AC是⊙O的弦,过点C的切线交AB的延长线于点D,若OD= ![]() ,求∠BAC的度数.
,求∠BAC的度数. 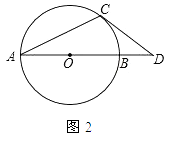
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、B、C在数轴上,O为原点,且BO:OC:CA=2:1:5.
(1)如果点C表示的数是x,请直接写出点A、B表示的数;
(2)如果点A表示的数比点C表示的数两倍还大4,求线段AB的长.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,方格纸中小正方形的边长为1,△ABC的三个顶点都在小正方形的格点上,求:
(1)边AC,AB,BC的长;
(2)点C到AB边的距离;
(3)求△ABC的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°,点P为射线BD,CE的交点.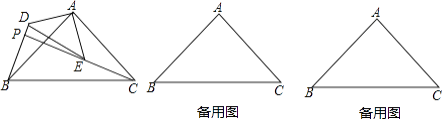
(1)求证:BD=CE;
(2)若AB=2,AD=1,把△ADE绕点A旋转,
①当∠EAC=90°时,求PB的长;
②直接写出旋转过程中线段PB长的最小值与最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
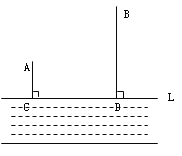
【题目】如图,A、B两个小集镇在河流CD的同侧,分别到河的距离为AC=10千米,BD=30千米,且CD=30千米,现在要在河边建一自来水厂,向A、B两镇供水,铺设水管的费用为每千米3万,请你在河流CD上选择水厂的位置M,使铺设水管的费用最节省,并求出总费用是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,三角形ABC的三个顶点的位置如图所示,点A'的坐标是(-2,2),现将三角形ABC平移,使点A变换为点A',点B',C'分别是B,C的对应点.
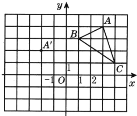
(1)请画出平移后的三角形A'B'C'(不写画法),并直接写出B',C'的坐标;
(2)若三角形ABC内部一点P的坐标为(a,b),则点P的对应点P'的坐标是_______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com