
【题目】如图,P为平行四边形ABCD的边AD上的一点,E,F分别为PB,PC的中点,△PEF,△PDC,△PAB的面积分别为S,S1 , S2 . 若S=3,则S1+S2的值为( ) 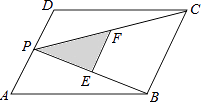
A.24
B.12
C.6
D.3
【答案】B
【解析】解:过P作PQ∥DC交BC于点Q, 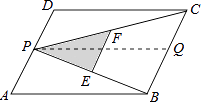
由DC∥AB,得到PQ∥AB,
∴四边形PQCD与四边形APQB都为平行四边形,
∴△PDC≌△CQP,△ABP≌△QPB,
∴S△PDC=S△CQP , S△ABP=S△QPB ,
∵EF为△PCB的中位线,
∴EF∥BC,EF= ![]() BC,
BC,
∴△PEF∽△PBC,且相似比为1:2,
∴S△PEF:S△PBC=1:4,S△PEF=3,
∴S△PBC=S△CQP+S△QPB=S△PDC+S△ABP=S1+S2=12.
故选:B.
【考点精析】本题主要考查了三角形中位线定理和平行四边形的性质的相关知识点,需要掌握连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半;平行四边形的对边相等且平行;平行四边形的对角相等,邻角互补;平行四边形的对角线互相平分才能正确解答此题.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案科目:初中数学 来源: 题型:
【题目】“世界那么大,我想去看看”一句话红遍网络,骑自行车旅行越来越受到人们的喜爱,各种品牌的山地自行车相继投放市场.某车行经营的A型车2016年4月份销售总额为3.2万元,今年经过改造升级后A型车每辆销售价比去年增加400元,若今年4月份与去年4月份卖出的A型车数量相同,则今年4月份A型车销售总额将比去年4月份销售总额增加25%.(A、B两种型号车今年的进货和销售价格如下表所示)
A型车 | B型车 | |
进货价格(元/辆) | 1100 | 1400 |
销售价格(元/辆) | 今年的销售价格 | 2400 |
(1)求今年4月份A型车每辆销售价多少元(用列方程进行解答);
(2)该车行计划5月份新进一批A型车和B型车共50辆,设购进的A型车为x辆,获得的总利润为y元,请写出y与x之间的函数关系式;
(3)在(2)的条件下,若B型车的进货数量不超过A型车数量的两倍,应如何进货才能使这批车获利最大?最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,AB的垂直平分线分别交AB,AC于点D,E.
(1)若∠A=40°,求∠EBC的度数;
(2)若AD=5,△EBC的周长为16,求△ABC的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图,A、B、C分别为数轴上的三点,A点对应的数为-200,B点对应的数为-20,C点对应的数为40.甲从C点出发,以6单位/秒的速度向左运动.
(1)当甲在B点、C点之间运动时,设运时间为x秒,请用x的代数式表示:
甲到A点的距离: ;
甲到B点的距离: ;
甲到C点的距离: .
(2)当甲运动到B点时,乙恰好从A点出发,以4单位/秒的速度向右运动,设两人在数轴上的D点相遇,求D点对应的数;
(3)若当甲运动到B点时,乙恰好从A点出发,以4单位/秒的速度向左运动,设两人在数轴上的E点相遇,求E点对应的数.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南水北调中线工程北京段干线工程起自房山北拒马河,经房山区至大宁水库,穿永定河,过丰台,沿西四环路北上至终点颐和园团城湖,全长80公里. 主要采取地下涵管压力输水方式,在输水过程中全程计量、跟踪监测、精细调度、高效配置,确保最大限度利用南水. 北京严格遵循南水北调工程“三先三后”原则,科学制定用水计划,研究确立了“节、喝、存、补”的用水方针,2017-2018年度入京水量达12.10亿立方米,成为历年来北京调水最多的一个调水年度. 如图,在铺设地下管道的时候,需要把拒马河沿线的管道l中的水引到房山水站A,B两处.

工人师傅设计了一种最节省材料的修建方案如下:


请回答:工人师傅的画图依据是___________.
查看答案和解析>>
科目:初中数学 来源: 题型:
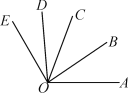
【题目】如图,OB是∠AOC的平分线,OD是∠COE的平分线.
(1)如果∠AOC=70°,∠COE=50°,那么∠BOD是多少度?
(2)如果∠BOD=70°,那么∠AOE是多少度?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:抛物线y=ax2+bx+c交y轴于点C(0,4),对称轴x=2与x轴交于点D,顶点为M,且DM=OC+OD, 
(1)求抛物线的解析式;
(2)设点P(x,y)是第一象限内该抛物线上的一个动点,△PCD的面积为S,求S关于x的函数关系式,写出自变量x的取值范围,并求当x取多少时,S的值最大,最大是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com