
����Ŀ��ʮ��������ʿ��ѧ��ŷ��֤���˼������ж�����(V)������(F)������(E)֮����ڵ�һ����Ȥ�Ĺ�ϵʽ������Ϊŷ����ʽ������۲����м��ּĶ�����ģ�ͣ�����������⣺
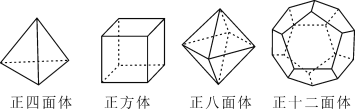
(1)��������Ķ�����ģ�ͣ���ɱ���
������ | ������(V) | ����(F) | ����(E) |
������ | 4 | 4 | |
������ | 8 | 12 | |
�������� | 6 | 8 | 12 |
��ʮ������ | 20 | 12 | 30 |
���Է��ֶ�����(V)������(F)������(E)֮����ڵĹ�ϵʽ��_______________��
(2)��һ��������������ȶ�������8������30���⣬������������������______��
(3)ij��������Ʒ�������Ǽ����壬������������������κͰ˱������ֶ����ƴ�Ӷ��ɣ�����24�����㣬ÿ�����㴦��3���⣮��ö���������������εĸ���Ϊx���˱��εĸ���Ϊy����x��y��ֵ��
���𰸡�(1)6,6,V��F��E��2 ;(2)20;(3)x��y��F��14
��������
��1���ӱ���۲췢�֣�������+����-����=2����2�����루1���е�ʽ�Ӽ��ɵõ���������3���õ�����������������������Ϊx+y��ֵ��
�⣺��1�������������Ϊ6����������Ķ�����Ϊ6����ϵʽΪ��V+F-E=2��
��2��������ã�F-8+F-30=2�����F=20��
��3������24�����㣬ÿ�����㴦����3���⣬����ȷ��һ��ֱ�ߣ�
���24��3��2=36���⣬
��ô24+F-36=2�����F=14��
��x+y=14��
�ʴ�Ϊ��6��6��E=V+F-2��20��14��


 ���ɶ��ȫ���ƿؾ�ϵ�д�
���ɶ��ȫ���ƿؾ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������ˮƽ�ߺ���ֱ�߽�ƽ��ֳ����ɸ����Ϊ1��С�����θ��ӣ�С�����εĶ���и�㣬�Ը��Ϊ����Ķ���νи�����Σ��������ε����ΪS���������ϸ��ĸ�����Ϊx��������ڲ��ĸ����Ϊn��S��x��n֮���Ƿ����һ����������ϵ�أ� 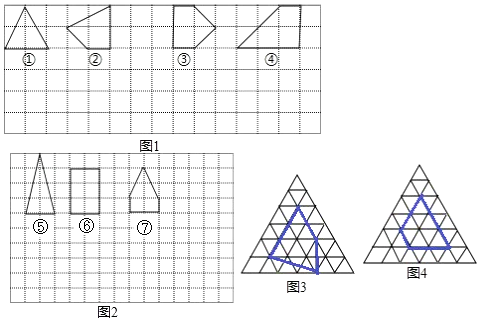
��1������̽����
��ͼ1��ͼ����ʾ�ĸ�����Σ����ڲ���ֻ��һ����㣬���ǵ����������ϸ��ĸ����͵Ķ�Ӧ��ϵ���±�������д�±���д��S��x֮��Ĺ�ϵʽS= ��
������� | �� | �� | �� | �� | �� |
�������S | 2 | 2.5 | 3 | 4 | �� |
�����ϸ��ĸ�����x | 4 | �� |
��2����ͼ2����ʾ�ĸ�����Σ���Щ������ڲ�������ֻ��2����㣮̽����ʱ�����ĸ�������ε����S���������ϸ��ĸ�����x֮��Ĺ�ϵʽS= ��
��3�������̽��������������ڲ�����ֻ��n��n���������������ʱ������S��x��n֮��Ĺ�ϵʽS=���ú�����ĸx��n�Ĵ���ʽ��ʾ��
��4��������չ��
�����������������е������������̽������ͼ3��4����������������ÿ��С�����������Ϊ1��С�������εĶ���Ϊ��㣬�Ը��Ϊ����Ķ���γ�Ϊ������Σ�ͼ�Ǹ��������θ���е���������Σ�
����ͼ���ṩ����Ϣ�����
������θ����ϵĸ��ĸ��� | ��������ڲ��ĸ����� | ������ε���� | |
�����1��ͼ3�� | 8 | 1 | 8 |
�����2��ͼ4�� | 7 | 3 | 11 |
�� | �� | �� | �� |
�� | �� | �� | �� |
�� | �� | �� | �� |
һ�������� | a | b | S |
��S��a��b֮��Ĺ�ϵΪS=���ú�a��b�Ĵ���ʽ��ʾ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
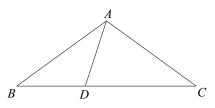
����Ŀ����ͼ������ABC�У�D��BC����һ�㣬AD=BD��AB=AC=CD������BAC�Ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=ax2+bx+c��x�ύ�ڵ�A����1��0����B��4��0������y�ύ�ڵ�C��0��2������D���C����x��Գƣ���P��x���ϵ�һ�����㣬���P������Ϊ��m��0��������P��x��Ĵ���l�����������ڵ�Q��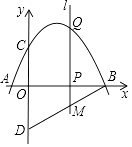
��1���������ߵĽ���ʽ��
��2����ֱ��BD�Ľ���ʽ��
��3������P���߶�OB���˶�ʱ��ֱ��l��BD�ڵ�M���Ƿ���ڵ�P��ʹ���ı���CQMD��ƽ���ı��Σ������ڣ����m��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
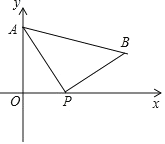
����Ŀ����ͼ��A��0��4����ֱ������ϵ y ����һ�㣬���� P ��ԭ�� O �������� x ���������˶����ٶ�Ϊÿ�� 1 ����λ���ȣ���PΪֱ�Ƕ����ڵ�һ������������Rt��APB����P����˶�ʱ��Ϊ t �룮
��1���� AB��x �ᣬ�� t ��ֵ��
��2����OP=![]() OA����B������꣮
OA����B������꣮
��3���� t=3 ʱ��x �����Ƿ������һ�� M��ʹ���� M��P��A Ϊ������������ǵ��������Σ���ֱ��д���� M �����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���A��0��6����B��8��0����AB=10����ͼ����DBO=��ABO����CAy=��BAO��BD��y���ڵ�E��ֱ��DO��AC�ڵ�C��
��1������֤����ACO�ա�EDO��������߶�AC��BD��λ�ù�ϵ��������ϵ��
��2������P��A��������A��O��B·���˶����ٶ�Ϊ1����B�㴦ֹͣ�˶�������Q��B��������B��O��A�˶����ٶ�Ϊ2����A�㴦ֹͣ�˶�������ͬʱ��ʼ�˶�����Ҫ������Ӧ���յ����ֹͣ����ijʱ�̣���PE��CD�ڵ�E��QF��CD�ڵ�F�����������˶��ʱ��ʱ��OPE���OQFȫ�ȣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���BAC=90�㣬����AMƽ�֡�BAC��AB=8��cos��ACB= ![]() ����PΪ����AM��һ�㣬��PB=PC�����ı���ABPC�����Ϊ ��
����PΪ����AM��һ�㣬��PB=PC�����ı���ABPC�����Ϊ �� 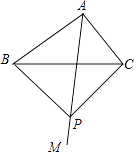
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com