练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

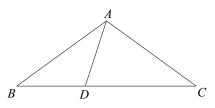
    【题目】如图，在△ABC中，D是BC边上一点，AD=BD，AB=AC=CD，求∠BAC的度数.

    【答案】108°.

    【解析】

    试题先设∠B=x，由AB=AC可知，∠C=x，由AD=DB可知∠B=∠DAB=x，由三角形外角的性质可知∠ADC=∠B+∠DAB=2x，根据AB=CD可知∠ADC=∠CAD=2x，再在△ACD中，由三角形内角和定理即可得出关于x的一元一次方程，求出x的值即可．

    试题解析：设∠B=x，∵AB=AC，∴∠C=∠B=x，∵AD=DB，∴∠B=∠DAB=x，∴∠ADC=∠B+∠DAB=2x，∵AB=CD，∴∠ADC=∠CAD=2x，在△ACD中，∠C=x，∠ADC=∠CAD=2x，∴x+2x+2x=180°，解得x=36°．∴∠ABC=36°．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图1，P点从点A开始以2厘米/秒的速度沿A→B→C的方向移动，点Q从点C开始以1厘米/秒的速度沿C→A→B的方向移动，在直角三角形ABC中，∠A＝90°，若AB＝16厘米，AC＝12厘米，BC＝20厘米，如果P、Q同时出发，用t（秒）表示移动时间，那么：

    （1）如图1，若P在线段AB上运动，Q在线段CA上运动，试求出t为何值时，QA＝AP

    （2）如图2，点Q在CA上运动，试求出t为何值时，三角形QAB的面积等于三角形ABC面积的；

    （3）如图3，当P点到达C点时，P、Q两点都停止运动，试求当t为何值时，线段AQ的长度等于线段BP的长的

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】随着全国各地空气出现严重污染，PM2.5屡屡爆表，我国多个城市发生雾霾天气，越来越多的人开始关注一个原本陌生的术语﹣PM2.5．某校九年级共有1000名学生，团委准备调查他们对“PM2.5”知识的了解程度．
    （1）在确定调查方式时，团委设计了以下三种方案： 方案一：调查九年级部分女生；
    方案二：调查九年级部分男生；
    方案三：到九年级每个班去随机调查一定数量的学生．
    请问其中最具有代表性的一个方案是；
    （2）团委采用了最具有代表性的调查方案，并用收集到的数据绘制出两幅不完整的统计图，请你根据图中信息，将其补充完整；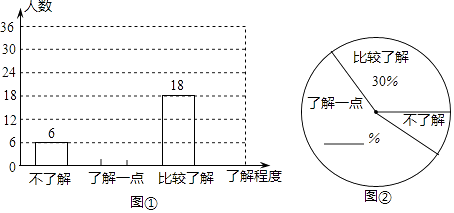
    （3）请你估计该校九年级约有多少名学生比较了解“PM2.5”的知识．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：在四边形ABCD中，对角线AC、BD相交于点E，且AC⊥BD，作BF⊥CD，垂足为点F，BF与AC交于点C，∠BGE=∠ADE．

    （1）如图1，求证：AD=CD；

    （2）如图2，BH是△ABE的中线，若AE=2DE，DE=EG，在不添加任何辅助线的情况下，请直接写出图2中四个三角形，使写出的每个三角形的面积都等于△ADE面积的2倍．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，AB∥CD，∠1=∠2，∠3=∠4．

    （1）求证：AD∥BE；

    （2）若∠B=∠3=2∠2，求∠D的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图：

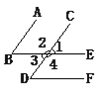
    （1）如果∠1＝∠B，那么_______∥_______，根据是__________________________；

    （2）如果∠3＝∠D，那么_______∥_______，根据是__________________________；

    （3）如果要使BE∥DF，必须∠1＝∠_______，根据是_________________________.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(V)、面数(F)、棱数(E)之间存在的一个有趣的关系式，被称为欧拉公式．请你观察下列几种简单的多面体模型，解答下列问题：

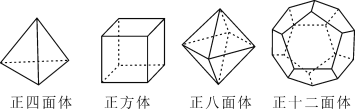
    (1)根据上面的多面体模型，完成表格：

    多面体

    顶点数(V)

    面数(F)

    棱数(E)

    四面体

    4

    4

    正方体

    8

    12

    正八面体

    6

    8

    12

    正十二面体

    20

    12

    30

    可以发现顶点数(V)、面数(F)、棱数(E)之间存在的关系式是_______________；

    (2)若一个多面体的面数比顶点数大8，且有30条棱，则这个多面体的面数是______；

    (3)某个玻璃饰品的外形是简单多面体，它的外表面是由三角形和八边形两种多边形拼接而成，且有24个顶点，每个顶点处有3条棱．设该多面体外表面三角形的个数为x，八边形的个数为y，求x＋y的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】先化简，再求值

    （1）[（x﹣y）2+（x+y）（x﹣y）]÷2x，其中x=3，y=1.5

    （2）（+m﹣2）÷，其中m=﹣．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，⊙O的半径是2，AB是⊙O的弦，点P是弦AB上的动点，且1≤OP≤2，则弦AB所对的圆周角的度数是（ ）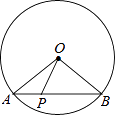
    A.60°
    B.120°
    C.60°或120°
    D.30°或150°

    查看答案和解析>>

    同步练习册答案