
【题目】已知:在四边形ABCD中,对角线AC、BD相交于点E,且AC⊥BD,作BF⊥CD,垂足为点F,BF与AC交于点C,∠BGE=∠ADE.
(1)如图1,求证:AD=CD;
(2)如图2,BH是△ABE的中线,若AE=2DE,DE=EG,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于△ADE面积的2倍.

【答案】(1)证明见解析;(2)△ACD、△ABE、△BCE、△BHG.
【解析】(1)由AC⊥BD、BF⊥CD知∠ADE+∠DAE=∠CGF+∠GCF,根据∠BGE=∠ADE=∠CGF得出∠DAE=∠GCF即可得;
(2)设DE=a,先得出AE=2DE=2a、EG=DE=a、AH=HE=a、CE=AE=2a,据此知S△ADC=2a2=2S△ADE,证△ADE≌△BGE得BE=AE=2a,再分别求出S△ABE、S△ACE、S△BHG,从而得出答案.
(1)∵∠BGE=∠ADE,∠BGE=∠CGF,
∴∠ADE=∠CGF,
∵AC⊥BD、BF⊥CD,
∴∠ADE+∠DAE=∠CGF+∠GCF,
∴∠DAE=∠GCF,
∴AD=CD;
(2)设DE=a,
则AE=2DE=2a,EG=DE=a,
∴S△ADE=![]() AE×DE=
AE×DE=![]() ×2a×a=a2,
×2a×a=a2,
∵BH是△ABE的中线,
∴AH=HE=a,
∵AD=CD、AC⊥BD,
∴CE=AE=2a,
则S△ADC=![]() ACDE=
ACDE=![]() (2a+2a)a=2a2=2S△ADE;
(2a+2a)a=2a2=2S△ADE;
在△ADE和△BGE中,
∵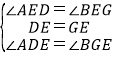 ,
,
∴△ADE≌△BGE(ASA),
∴BE=AE=2a,
∴S△ABE=![]() AEBE=
AEBE=![]() (2a)2a=2a2,
(2a)2a=2a2,
S△ACE=![]() CEBE=
CEBE=![]() (2a)2a=2a2,
(2a)2a=2a2,
S△BHG=![]() HGBE=
HGBE=![]() (a+a)2a=2a2,
(a+a)2a=2a2,
综上,面积等于△ADE面积的2倍的三角形有△ACD、△ABE、△BCE、△BHG.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,直线AB、CD相交于点O,下列条件中,不能说明AB⊥CD的是( )

A. ∠AOD=90°
B. ∠AOC=∠BOC
C. ∠BOC+∠BOD=180°
D. ∠AOC+∠BOD=180°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市在一次市政施工中,有两段长度相等的人行道铺设任务,分别交给甲、乙两个施工队同时进行施工.如图是反映所铺设人行道的长度y(米)与施工时间x(时)之间关系的部分图象.请解答下列问题: 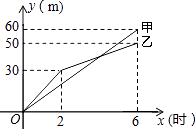
(1)求乙队在2≤x≤6的时间段内,y与x的函数关系式;
(2)若甲队施工速度不变,乙队在施工6小时后,施工速度增加到12米/时,结果两队同时完成了任务.求甲队从开始施工到完成,所铺设的人行道共是多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题提出:用水平线和竖直线将平面分成若干个面积为1的小长方形格子,小长方形的顶点叫格点,以格点为顶点的多边形叫格点多边形.设格点多边形的面积为S,它各边上格点的个数和为x,多边形内部的格点数为n,S与x,n之间是否存在一定的数量关系呢? 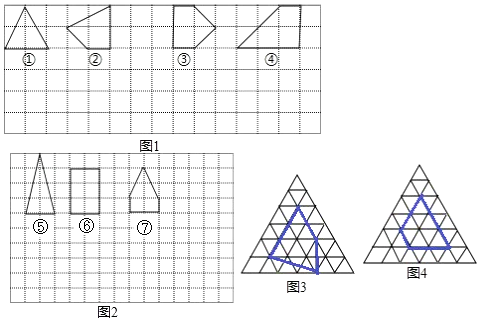
(1)问题探究:
如图1,图中所示的格点多边形,其内部都只有一个格点,它们的面积与各边上格点的个数和的对应关系如下表,请填写下表并写出S与x之间的关系式S= .
多边形的序号 | ① | ② | ③ | ④ | … |
多边形的面积S | 2 | 2.5 | 3 | 4 | … |
各边上格点的个数和x | 4 | … |
(2)在图2中所示的格点多边形,这些多边形内部都有且只有2个格点.探究此时所画的各个多边形的面积S与它各边上格点的个数和x之间的关系式S= .
(3)请继续探索,当格点多边形内部有且只有n(n是正整数)个格点时,猜想S与x,n之间的关系式S=(用含有字母x,n的代数式表示)
(4)问题拓展:
请在正三角形网格中的类似问题进行探究:在图3、4中正三角形网格中每个小正三角形面积为1,小正三角形的顶点为格点,以格点为顶点的多边形称为格点多边形,图是该正三角形格点中的两个多边形.
根据图中提供的信息填表:
格点多边形各边上的格点的个数 | 格点多边形内部的格点个数 | 格点多边形的面积 | |
多边形1(图3) | 8 | 1 | 8 |
多边形2(图4) | 7 | 3 | 11 |
… | … | … | … |
… | … | … | … |
… | … | … | … |
一般格点多边形 | a | b | S |
则S与a,b之间的关系为S=(用含a,b的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1.在菱形ABCD中,AB=2 ![]() ,tan∠ABC=2,∠BCD=α,点E从点D出发,以每秒1个单位长度的速度沿着射线DA的方向匀速运动,设运动时间为t(秒),将线段CE绕点C顺时针旋转α度,得到对应线段CF,连接BD、EF,BD交EC、EF于点P、Q.
,tan∠ABC=2,∠BCD=α,点E从点D出发,以每秒1个单位长度的速度沿着射线DA的方向匀速运动,设运动时间为t(秒),将线段CE绕点C顺时针旋转α度,得到对应线段CF,连接BD、EF,BD交EC、EF于点P、Q.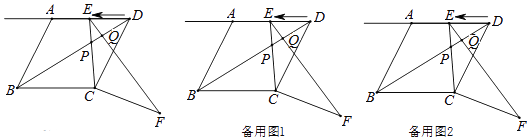
(1)求证:△ECF∽△BCD;
(2)当t为何值时,△ECF≌△BCD?
(3)当t为何值时,△EPQ是直角三角形?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com