
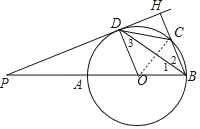
【题目】如图,在⊙O中,点P为直径BA延长线上一点,PD切⊙O于点D、过点B作BH⊥PH,点H为垂足,BH交⊙O于点C,连接BD,CD.
(1)求证:BD平分∠ABH;
(2)若CD=2,∠ABD=30°,求⊙O的直径的长.

【答案】(1)证明见解析;(2)4;
【解析】
(1)利用切线性质得OD⊥PH,则可证明BH∥OD,利用平行线的性质得∠2=∠3,加上∠1=∠3,从而得到∠1=∠2;
(2)连接OC,如图,先证明△OCB为等边三角形得到∠BOC=60°,再利用平行线的性质得到∠BOD=120°,所以∠DOC=60°,然后判定△OCD为等边三角形,则OD=CD=2,从而得到⊙O的直径的长.
(1)证明:∵PD切⊙O于点D,
∴OD⊥PH,
∵BH⊥PH,
∴BH∥OD,
∴∠2=∠3,
∵OD=OB,
∴∠1=∠3,
∴∠1=∠2,
∴BD平分∠ABH;
(2)解:连接OC,如图,
∵∠1=30°,
∴∠2=∠3=30°,
∴∠OBC=60°,
∴△OCB为等边三角形,
∴∠BOC=60°,
∵BC∥OD,
∴∠BOD=180°﹣∠OBC=120°,
∴∠DOC=60°,
而OC=OD,
∴△OCD为等边三角形,
∴OD=CD=2,
∴⊙O的直径的长为4.


 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案科目:初中数学 来源: 题型:
【题目】某商场经营某种品牌的玩具,购进时的单价是30元,根据市场调查:在一段时间内,销售单价是40元时,销售量是600件,而销售单价每涨1元,就会少售出10件玩具.
(1)不妨设该种品牌玩具的销售单价为x元(x>40),请你分别用x的代数式来表示销售量y件和销售该品牌玩具获得利润w元,并把结果填写在表格中:
销售单价(元) | x |
销售量y(件) |
|
销售玩具获得利润w(元) |
|
(2)在(1)问条件下,若商场获得了10000元销售利润,求该玩具销售单价x应定为多少元.
(3)在(1)问条件下,若玩具厂规定该品牌玩具销售单价不低于44元,且商场要完成不少于540件的销售任务,求商场销售该品牌玩具获得的最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把矩形纸片ABCD沿EF翻折,点A恰好落在BC边的A′处,若AB= ![]() ,∠EFA=60°,则四边形A′B′EF的周长是( )
,∠EFA=60°,则四边形A′B′EF的周长是( )

A. 1+3![]() B. 3+
B. 3+![]() C. 4+
C. 4+![]() D. 5+
D. 5+![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,MN是⊙O的直径,∠AMN=40°,点B为弧AN的中点,点P是直径MN上的一个动点,如果PA+PB的最小值为![]() ,那么⊙O的直径等于( )
,那么⊙O的直径等于( )
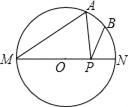
A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在半径为4的⊙O中,圆心角∠AOB=90°,以半径OA、OB的中点C、F为顶点作矩形CDEF,顶点D、E在⊙O的劣弧![]() 上,OM⊥DE于点M.试求图中阴影部分的面积.(结果保留π)
上,OM⊥DE于点M.试求图中阴影部分的面积.(结果保留π)

查看答案和解析>>
科目:初中数学 来源: 题型:
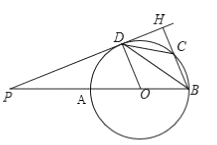
【题目】如图,在⊙O中,点P为直径BA延长线上一点,PD切⊙O于点D、过点B作BH⊥PH,点H为垂足,BH交⊙O于点C,连接BD,CD.
(1)求证:BD平分∠ABH;
(2)若CD=2,∠ABD=30°,求⊙O的直径的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
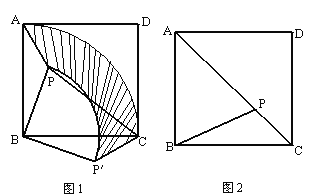
【题目】已知,点P是正方形ABCD内的一点,连PA、PB、PC.
(1)将△PAB绕点B顺时针旋转90°到△P′CB的位置(如图1).
①设AB的长为a,PB的长为b(b<a),求△PAB旋转到△P′CB的过程中边PA所扫过区域(图1中阴影部分)的面积;
②若PA=2,PB=4,∠APB=135°,求PC的长.
(2)如图2,若PA2+PC2=2PB2,请说明点P必在对角线AC上.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com