
【题目】如图,在⊙O中,点P为直径BA延长线上一点,PD切⊙O于点D、过点B作BH⊥PH,点H为垂足,BH交⊙O于点C,连接BD,CD.
(1)求证:BD平分∠ABH;
(2)若CD=2,∠ABD=30°,求⊙O的直径的长.
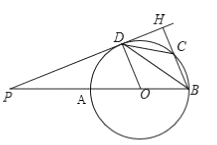
【答案】(1)证明见解析;(2)4;
【解析】
(1)利用切线性质得OD⊥PH,则可证明BH∥OD,利用平行线的性质得∠2=∠3,加上∠1=∠3,从而得到∠1=∠2;
(2)连接OC,如图,先证明△OCB为等边三角形得到∠BOC=60°,再利用平行线的性质得到∠BOD=120°,所以∠DOC=60°,然后判定△OCD为等边三角形,则OD=CD=2,从而得到⊙O的直径的长.
(1)证明:∵PD切⊙O于点D,
∴OD⊥PH,
∵BH⊥PH,
∴BH∥OD,
∴∠2=∠3,
∵OD=OB,
∴∠1=∠3,
∴∠1=∠2,
∴BD平分∠ABH;
(2)解:连接OC,如图,
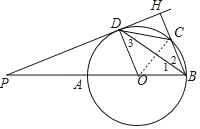
∵∠1=30°,
∴∠2=∠3=30°,
∴∠OBC=60°,
∴△OCB为等边三角形,
∴∠BOC=60°,
∵BC∥OD,
∴∠BOD=180°﹣∠OBC=120°,
∴∠DOC=60°,
而OC=OD,
∴△OCD为等边三角形,
∴OD=CD=2,
∴⊙O的直径的长为4.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
![]() 如图①,在
如图①,在![]() 中,
中,![]() 为角平分线,
为角平分线,![]() ,
,![]() ,求证:
,求证:![]() 是
是![]() 的完美分割线;
的完美分割线;
![]() 如图②,在
如图②,在![]() 中,
中,![]() ,
,![]() ,
,![]() 是
是![]() 的完美分割线,且
的完美分割线,且![]() 是以
是以![]() 为底边的等腰三角形,求完美分割线
为底边的等腰三角形,求完美分割线![]() 的长.
的长.
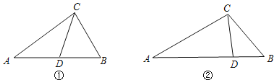
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在⊙O中,点P为直径BA延长线上一点,PD切⊙O于点D、过点B作BH⊥PH,点H为垂足,BH交⊙O于点C,连接BD,CD.
(1)求证:BD平分∠ABH;
(2)若CD=2,∠ABD=30°,求⊙O的直径的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为缓解油价上涨给出租车待业带来的成本压力,某巿自2018年11月17日起,调整出租车运价,调整方案见下列表格及图象(其中a,b,c为常数)
行驶路程 | 收费标准 | |
调价前 | 调价后 | |
不超过3km的部分 | 起步价6元 | 起步价a 元 |
超过3km不超出6km的部分 | 每公里2.1元 | 每公里b元 |
超出6km的部分 | 每公里c元 | |
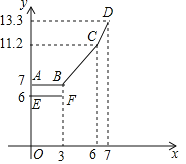
设行驶路程xkm时,调价前的运价y1(元),调价后的运价为y2(元)如图,折线ABCD表示y2与x之间的函数关系式,线段EF表示当0≤x≤3时,y1与x的函数关系式,根据图表信息,完成下列各题:
(1)填空:a= ,b= ,c= .
(2)写出当x>3时,y1与x的关系,并在上图中画出该函数的图象.
(3)函数y1与y2的图象是否存在交点?若存在,求出交点的坐标,并说明该点的实际意义,若不存在请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,平面直角坐标系中,点A(2,9),B(2,3),C(3,2),D(9,2)在⊙P上,Q是⊙P上的一个动点.
(1)在图中标出圆心P位置,写出点P坐标;
(2)Q点在圆上坐标为何值时,△ABQ是直角三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的一条弦,OD⊥AB,垂足为点C,交⊙O于点D,点E在⊙O上.
(1)若∠AOD=52°,求∠DEB的度数;
(2)若CD=2,AB=8,求半径的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知直线![]() 交
交![]() 轴、
轴、![]() 轴分别于
轴分别于![]() 两点,平行于
两点,平行于![]() 轴的直线
轴的直线![]() 从点
从点![]() 开始以每秒
开始以每秒![]() 个单位的速度向
个单位的速度向![]() 轴的负方向运动,直线
轴的负方向运动,直线![]() 交
交![]() 轴于点
轴于点![]() ,交直线
,交直线![]() 于点
于点![]() ,设直线
,设直线![]() 的运动时间为
的运动时间为![]() 秒.
秒.

![]() 求线段
求线段![]() 的长.
的长.
![]() 若
若![]() 为直线
为直线![]() 上一动点,将
上一动点,将![]() 沿着
沿着![]() 翻折,当点
翻折,当点![]() 的对应点
的对应点![]() 落在直线
落在直线![]() 上时,求直线
上时,求直线![]() 的解析式.
的解析式.
![]() 若
若![]() 为
为![]() 的中点,当
的中点,当![]() 是等腰三角形时,求
是等腰三角形时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人在笔直的湖边公路上同起点、同终点、同方向匀速步行2400米,先到终点的人原地休息.已知甲先出发4分钟,在整个步行过程中,甲、乙两人的距离y(米)与甲出发的时间t(分)之间的关系如图所示,下列结论:
①甲步行的速度为60米/分;
②乙走完全程用了32分钟;
③乙用16分钟追上甲;
④乙到达终点时,甲离终点还有300米
其中正确的结论有( )

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,点![]() ,点
,点![]() ,若动点
,若动点![]() 从坐标原点出发,沿
从坐标原点出发,沿![]() 轴正方向匀速运动,运动速度为
轴正方向匀速运动,运动速度为![]() ,设点
,设点![]() 运动时间为
运动时间为![]() 秒,当
秒,当![]() 是以
是以![]() 为腰的等腰三角形时,直接写出
为腰的等腰三角形时,直接写出![]() 的所有值__________________.
的所有值__________________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com